题目内容
 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=考点:与圆有关的比例线段
专题:立体几何
分析:利用四边形OABC为平行四边形,可得∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.利用四边形ABCD是圆的内接四边形,可得∠D+∠B=180°.利用同弧所对的圆周角和圆心角可得∠D=
∠AOC,进而即可得出.
| 1 |
| 2 |
解答:
解:∵四边形OABC为平行四边形,
∴∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.
∵四边形ABCD是圆的内接四边形,
∴∠D+∠B=180°.
又∠D=
∠AOC,
∴3∠D=180°,解得∠D=60°.
∴∠OAB=∠OCB=180°-∠B=60°.
∴∠OAD+∠OCD=360°-(∠D+∠B+∠OAB+∠OCB)=360°-(60°+120°+60°+60°)=60°.
故答案为:60°.
∴∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.
∵四边形ABCD是圆的内接四边形,
∴∠D+∠B=180°.
又∠D=
| 1 |
| 2 |
∴3∠D=180°,解得∠D=60°.
∴∠OAB=∠OCB=180°-∠B=60°.
∴∠OAD+∠OCD=360°-(∠D+∠B+∠OAB+∠OCB)=360°-(60°+120°+60°+60°)=60°.
故答案为:60°.
点评:本题考查了平行四边形的性质、圆的内接四边形的性质、同弧所对的圆周角和圆心角的关系,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=b
,在直角坐标平面内,已知点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn)…,则向量
+
+
+…+
的坐标为( )
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、(3015,8[(
| ||
B、(3012,8[(
| ||
C、(3015,8[(
| ||
D、(3018,8[(
|
函数f(x)=2x2-kx-8在区间[1,2]上不单调,则实数k的取值范围为( )
| A、[4,8] |
| B、(-∞,4]∪[8,+∞) |
| C、(-∞,4)∪(8,+∞) |
| D、(4,8) |
在面积为1的正方形ABCD内部随机取一点P,则△PAB的面积大于等于
的概率是( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
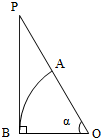 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
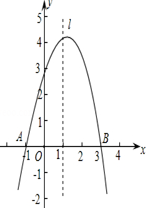 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.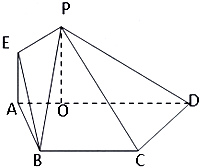 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,