题目内容
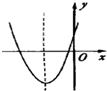二次函数y=ax2+bx+c的图象如图所示，则a+b+c考点：二次函数的性质
专题：函数的性质及应用
分析：结合二次函数的图象与性质，得出f（1）＞0；与x轴有不同的两个交点，得出△＞0．
解答：
解：由二次函数y=ax2+bx+c的图象知，
图象开口向上，且与x轴有不同的两个交点，
∴b2-4ac＞0；
又二次函数图象的对称轴在y轴的左侧，且f（0）＞0，
∴f（1）＞f（0）＞0；
即a+b+c＞0；
故答案为：＞，＞．
图象开口向上，且与x轴有不同的两个交点，
∴b2-4ac＞0；
又二次函数图象的对称轴在y轴的左侧，且f（0）＞0，
∴f（1）＞f（0）＞0；
即a+b+c＞0；
故答案为：＞，＞．
点评：本题考查了二次函数的图象与性质应用问题，是基础题．
练习册系列答案
海淀黄冈名师导航系列答案
相关题目
过点M（-1，m），N（m+1，4）的直线的斜率等于1，则m的值为（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
设函数f(x)=
（a∈R）．若方程f（f（x））=x有解，则a的取值范围为（ ）
| x-a |
A、(-∞，
| ||
B、(0，
| ||
C、(-∞，
| ||
| D、[1，+∞） |
数列{an}中a1=1，a5=13，an+2+an=2an+1；数列{bn}中，b2=6，b3=3，bn+2bn=b
，在直角坐标平面内，已知点列P1（a1，b1），P2（a2，b2），P3（a3，b3），…，Pn（an，bn）…，则向量
+
+
+…+
的坐标为（ ）
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、（3015，8[（
| ||
B、（3012，8[（
| ||
C、（3015，8[（
| ||
D、（3018，8[（
|
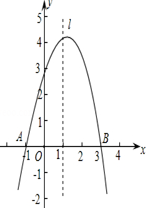已知抛物线y=ax2+bx+c经过A（-1，0）、B（3，0）、C（0，3）三点，直线l是抛物线的对称轴．