Question

14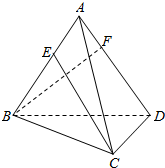．如图：正三棱锥ABCD中，E、F分别在棱AB、AD上，AE：EB=AF：FD=1：2，且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0，则∠BAC的余弦值为（　　）

• A． $\frac{1}{5}$
• B． $\frac{2}{7}$
• C． $\frac{3}{7}$
• D． $\frac{1}{2}$

Answer 1

分析 根据正三棱锥ABCD中，侧棱长相等，各侧棱所成的角相等，结合$\overrightarrow{CE}$•$\overrightarrow{BF}$=0，利用向量的线性表示，即可求出∠BAC的余弦值．

解答 解：正三棱锥ABCD中，设∠BAC=θ，且侧棱长相等；
∵AE：EB=AF：FD=1：2，
∴$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{3}$$\overrightarrow{AD}$；
又$\overrightarrow{CE}$•$\overrightarrow{BF}$=0，
∴（$\overrightarrow{CA}$+$\overrightarrow{AE}$）•（$\overrightarrow{BA}$+$\overrightarrow{AF}$）=0，
∴$\overrightarrow{CA}$•$\overrightarrow{BA}$+$\overrightarrow{CA}$•$\overrightarrow{AF}$+$\overrightarrow{AE}$•$\overrightarrow{BA}$+$\overrightarrow{AE}$•$\overrightarrow{AF}$=0，
∴|$\overrightarrow{CA}$|×|$\overrightarrow{BA}$|cosθ+|$\overrightarrow{CA}$|×$\frac{1}{3}$|$\overrightarrow{AD}$|cos（π-θ）-$\frac{1}{3}$|$\overrightarrow{AB}$|×|$\overrightarrow{BA}$|+$\frac{1}{3}$|$\overrightarrow{AB}$|×$\frac{1}{3}$|$\overrightarrow{AD}$|cosθ=0，
解得cosθ=$\frac{3}{7}$，
即∠BAC的余弦值为$\frac{3}{7}$．
故选：C．

点评 本题考查了空间向量的线性表示与数量积的运算问题，也考查了数形结合的应用问题，是基础题目．