题目内容
9.设等差数列{an}的前n项和为Sn,若S1=-2015,$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2,则S2015=( )| A. | 2014 | B. | 2015 | C. | -2014 | D. | -2015 |
分析 根据等差数列的前n项和Sn满足{$\frac{{S}_{n}}{n}$}也是等差数列,得出数列{$\frac{{S}_{n}}{n}$}是以-2015为首项,1为公差的等差数列,写出它的通项公式,从而求出答案.
解答 解:设等差数列{an}的前n项和Sn=An2+Bn,
则$\frac{{S}_{n}}{n}$=An+B,
∴{$\frac{{S}_{n}}{n}$}成等差数列;
又$\frac{{S}_{1}}{1}$=-2015,$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2,
∴{$\frac{{S}_{n}}{n}$}是以-2015为首项,以1为公差的等差数列;
∴$\frac{{S}_{2015}}{2015}$=-2015+(2015-1)×1=-1,
∴S2015=-2015.
故选:D.
点评 本题考查了等差数列的定义与前n项和公式的应用问题,解题时要认真审题,注意构造法的合理运用,是基础题目.

练习册系列答案
相关题目
14.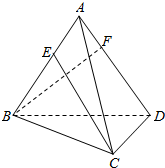 如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
 如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{2}$ |
1.函数f(x)=x|x+a|+b是奇函数,则( )
| A. | a•b=0 | B. | a+b=0 | C. | a2+b2=0 | D. | a=b |
8.在△ABC中,角A,B,C的对边分别为a,b,c,若$\frac{2a-c}{b}$=$\frac{cosC}{cosB}$,b=4,则△ABC的面积的最大值为( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |