题目内容
19．设a=-3${∫}_{\frac{π}{2}}^{\frac{3π}{2}}$cosxdx，则二项式（x2+x+y）a展开式中x7y2项的系数为（ ）| A． | 120 | B． | 80 | C． | 60 | D． | 50 |
分析 由条件利用定积分求得a的值，再利用二项式定理求得含x7y2项的系数．
解答 解：a=-3${∫}_{\frac{π}{2}}^{\frac{3π}{2}}$cosxdx=-3sinx${|}_{\frac{π}{2}}^{\frac{3π}{2}}$=-3（-1-1）=6，
则二项式（x2+x+y）a =（x2+x+y）6，
由于=（x2+x+y）6表示6个因式（x2+x+y）的积，故有2个因式取y，
其余的4个因式中有1个取x，有3个取x2，可得含x7y2项的系数．
故x7y2项的系数为 ${C}_{6}^{2}$•${C}_{4}^{1}$•${C}_{3}^{3}$=60，
故选：C．
点评 本题主要考查定积分的求法，本题主要考查二项式定理的应用，属于中档题．
练习册系列答案
相关题目
10．党的十八大提出，“富强、民主、文明、和谐，自由、平等、公正、法治，爱国、敬业、诚信、友善”为社会主义核心价值观．某地区为了响应党的号召，努力推行社会主义核心价值观，倡导人人学习，人人熟记核心价值观的内容．为此该地区对年龄在[15，75]的市民进行调查核心价值观的背诵情况．随机抽查了50人，并将抽查情况进行整理后制成如下表格：
年龄（岁数）
（1）请估计该地区年龄在[15，75]的市民对社会主义核心价值观的熟记的概率；
（2）若从年龄在[55，65）和[65，75]的凋查者中各随机选取2人进行追踪调查，记被选取的4人中没有熟记“社会主义核心价值观”的人数为X，求随机变量X的分布列和数学期望．
年龄（岁数）
| 年龄（岁数） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
| 频数 | 6 | 10 | 12 | 12 | 5 | 5 |
| 熟记人数 | 3 | 6 | 10 | 6 | 4 | 3 |
（2）若从年龄在[55，65）和[65，75]的凋查者中各随机选取2人进行追踪调查，记被选取的4人中没有熟记“社会主义核心价值观”的人数为X，求随机变量X的分布列和数学期望．
14．
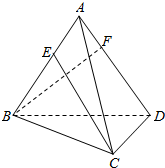如图：正三棱锥ABCD中，E、F分别在棱AB、AD上，AE：EB=AF：FD=1：2，且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0，则∠BAC的余弦值为（ ）
如图：正三棱锥ABCD中，E、F分别在棱AB、AD上，AE：EB=AF：FD=1：2，且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0，则∠BAC的余弦值为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{7}$ | C． | $\frac{3}{7}$ | D． | $\frac{1}{2}$ |
11．设各项均为正数的等比数列{an}的公比为q，若数列{log2a1an}为递减数列，则（ ）
| A． | 0＜q＜1 | B． | q＞1 | C． | 0＜a1q＜1 | D． | a1q＞1 |
8．若$\frac{3π}{2}$≤α≤2π，则$\sqrt{1+sinα}$+$\sqrt{1-sinα}$等于（ ）
| A． | 2cos$\frac{α}{2}$ | B． | -2cos$\frac{α}{2}$ | C． | 2sin$\frac{α}{2}$ | D． | -2sin$\frac{α}{2}$ |