题目内容
13.某三棱柱的三视图如图所示,则该三棱柱的体积为4.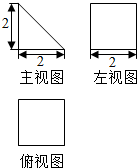
分析 三棱柱的底面为等腰直角三角形,棱柱的高为2,代入体积公式计算即可.
解答 解:由三视图可知三棱柱的底面为直角边为2等腰直角三角形,棱柱的高为2,这是一个歪放的三棱柱
∴V=$\frac{1}{2}×2×2×2$=4.
故答案为4.
点评 本题考查了棱柱的三视图及体积计算,属于基础题.

练习册系列答案
相关题目
14.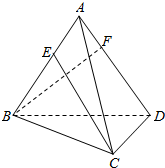 如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
 如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{2}$ |
8.在△ABC中,角A,B,C的对边分别为a,b,c,若$\frac{2a-c}{b}$=$\frac{cosC}{cosB}$,b=4,则△ABC的面积的最大值为( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
2.已知正四面体ABCD的棱长为a,其外接球表面积为S1,内切球表面积为S2,则S1:S2的值为( )
| A. | 3 | B. | $3\sqrt{3}$ | C. | 9 | D. | $\frac{49}{4}$ |
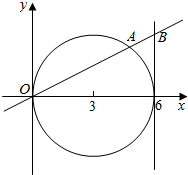 如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;
如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;