题目内容
6.已知方程x2+3x+c=0的两个根为x1、x2,且|x1-x2|=1.(1)若x1、x2是实数,求实数c的值;
(2)若x1、x2是复数,求实数c的值.
分析 根据根与系数的关系得出x1+x2=-3,x1x2=c;
(1)当x1、x2是实数时,利用${{(x}_{1}{-x}_{2})}^{2}$=${{(x}_{1}{+x}_{2})}^{2}$-4x1x2求出c的值;
(2)当x1、x2是复数时,设x1=-$\frac{3}{2}$+bi,则x2=-$\frac{3}{2}$-bi,利用|x1-x2|=1求出|b|的值,计算c的值即可.
解答 解:∵方程x2+3x+c=0的两个根为x1、x2,
∴x1+x2=-3,x1x2=c;
又|x1-x2|=1,
(1)若x1、x2是实数,
则${{(x}_{1}{-x}_{2})}^{2}$=${{(x}_{1}{+x}_{2})}^{2}$-4x1x2=(-3)2-4c=1,
解得c=2;
(2)若x1、x2是复数,
设x1=-$\frac{3}{2}$+bi,b∈R,
则x2=-$\frac{3}{2}$-bi;
∴|x1-x2|=|2bi|=2|b|=1,
解得|b|=$\frac{1}{2}$;
∴c=(-$\frac{3}{2}$+bi)(-$\frac{3}{2}$-bi)=$\frac{9}{4}$+b2=$\frac{9}{4}$+$\frac{1}{4}$=$\frac{5}{2}$.
点评 本题考查了实系数一元二次方程的解法与应用问题,也考查了根与系数的应用问题,是基础题目.

练习册系列答案
相关题目
14.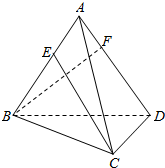 如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
 如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )
如图:正三棱锥ABCD中,E、F分别在棱AB、AD上,AE:EB=AF:FD=1:2,且$\overrightarrow{CE}$•$\overrightarrow{BF}$=0,则∠BAC的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{2}$ |
1.函数f(x)=x|x+a|+b是奇函数,则( )
| A. | a•b=0 | B. | a+b=0 | C. | a2+b2=0 | D. | a=b |
11.设各项均为正数的等比数列{an}的公比为q,若数列{log2a1an}为递减数列,则( )
| A. | 0<q<1 | B. | q>1 | C. | 0<a1q<1 | D. | a1q>1 |