题目内容
已知f(x)=
(1)若存在实数x0,使得f(x0)≤m,求m的取值范围;
(2)若x1≠x2且f(x1)=f(x2),求证:x1+x2<0.
|
(1)若存在实数x0,使得f(x0)≤m,求m的取值范围;
(2)若x1≠x2且f(x1)=f(x2),求证:x1+x2<0.
考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)若存在实数x0,使得f(x0)≤m,即f(x)min≤m,分析函数的单调性,进而求出最小值,即可得到m的取值范围;
(2)证法一:分析函数的单调性,根据x1≠x2且f(x1)=f(x2),令g(x)=f(-x),xx1<0<x2,分析g出g(-x1)<f(-x1),进而可得结论;
证法二:分析函数的单调性,根据x1≠x2且f(x1)=f(x2),令g(x)=f(-x),xx1<0<x2,判断出
+
=
>0,进而得到结论.
(2)证法一:分析函数的单调性,根据x1≠x2且f(x1)=f(x2),令g(x)=f(-x),xx1<0<x2,分析g出g(-x1)<f(-x1),进而可得结论;
证法二:分析函数的单调性,根据x1≠x2且f(x1)=f(x2),令g(x)=f(-x),xx1<0<x2,判断出
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
解答:
解:(1)因为(
)x在(-∞,0)上单调递减,
故x<0时,f(x)∈(1,+∞);
因为3x在[0,+∞)上单调递增,故x≥0时,f(x)∈[1,+∞),
故f(x)的值域为[1,+∞),
因为存在实数x0,使得f(x0)≤m,
故m≥1,
所以m的取值范围是[1,+∞);
(2)证法一:因为x1≠x2且f(x1)=f(x2)
而f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
故不妨设x1<0<x2,则-x1>0,
设g(x)=f(-x),故x>0时,
f(x)-g(x)=3x-(
)-x=3x-2x>0
所以f(x2)=f(x1)=g(-x1)<f(-x1),
又f(x)在(0,+∞)上单调递增,所以x2<-x1,
即x1+x2<0.
证法二:因为x1≠x2且f(x1)=f(x2)
而f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
故不妨设x1<0<x2,
设f(x1)=f(x2)=a,由(1)知,a>1,
故x1=log
a,x2=log3a,
所以
+
=loga
+loga3=loga
>0
即
>0,又x1x2<0,
所以x1+x2<0.
| 1 |
| 2 |
故x<0时,f(x)∈(1,+∞);
因为3x在[0,+∞)上单调递增,故x≥0时,f(x)∈[1,+∞),
故f(x)的值域为[1,+∞),
因为存在实数x0,使得f(x0)≤m,
故m≥1,
所以m的取值范围是[1,+∞);
(2)证法一:因为x1≠x2且f(x1)=f(x2)
而f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
故不妨设x1<0<x2,则-x1>0,
设g(x)=f(-x),故x>0时,
f(x)-g(x)=3x-(
| 1 |
| 2 |
所以f(x2)=f(x1)=g(-x1)<f(-x1),
又f(x)在(0,+∞)上单调递增,所以x2<-x1,
即x1+x2<0.
证法二:因为x1≠x2且f(x1)=f(x2)
而f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
故不妨设x1<0<x2,
设f(x1)=f(x2)=a,由(1)知,a>1,
故x1=log
| 1 |
| 2 |
所以
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| 2 |
| 3 |
| 2 |
即
| x1+x2 |
| x1x2 |
所以x1+x2<0.
点评:本题考查的知识点是函数单调性的性质,存在性问题,函数的最值,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
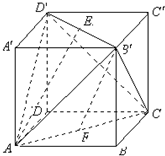 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求: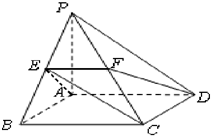 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,