题目内容
 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,CD=4,E、F分别为CD、PB的中点.
①求证:EF⊥平面PAB.
②求直线AE与平面PAB所成的角.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:①求出直线EF所在的向量,再求出平面内两条相交直线所在的向量,然后利用向量的数量积为0,根据线面垂直的判定定理得到线面垂直;
②由①知
=(0,1,1)是平面PAB的一个法向量,利用向量的夹角公式,可求直线AE与平面PAB所成的角.
②由①知
| EF |
解答:
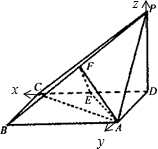 ①证明:以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D-xyz.
①证明:以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D-xyz.
则A(0,2,0),B(4,2,0),C(4,0,0),D(0,0,0,),P(0,0,2),E(2,0,0),F(2,1,1)
由题意可得:
•
=0×0+1×2+1×(-2)=0,
•
=0×a+1×2+1×(-2)=0
∴EF⊥PA,EF⊥PB.
∴EF⊥平面PAB;
②解:设直线AE与平面PAB为α,则
由①知
=(0,1,1)是平面PAB的一个法向量,
∵
=(2,-2,0),
∴sinα=|
|=
,
∴α=30°,
∴直线AE与平面PAB为30°.
 ①证明:以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D-xyz.
①证明:以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D-xyz.则A(0,2,0),B(4,2,0),C(4,0,0),D(0,0,0,),P(0,0,2),E(2,0,0),F(2,1,1)
由题意可得:
| EF |
| PA |
| EF |
| PB |
∴EF⊥PA,EF⊥PB.
∴EF⊥平面PAB;
②解:设直线AE与平面PAB为α,则
由①知
| EF |
∵
| AE |
∴sinα=|
| -2 | ||||
|
| 1 |
| 2 |
∴α=30°,
∴直线AE与平面PAB为30°.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
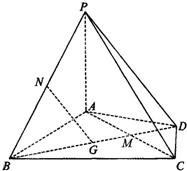 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且 对一根作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.
对一根作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.