题目内容
已知函数f(x)=2lnx-x2
(1)若方程f(x)+m=0在[
,e]内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)如果函数g(x)=f(x)-ax的图象与x轴交于两点A(x1,0)、B(x2,0)且0<x1<x2.求证:g′(px1+qx2)<0(其中正常数p,q满足p+q=1,且q≥p).
(1)若方程f(x)+m=0在[
| 1 |
| e |
(2)如果函数g(x)=f(x)-ax的图象与x轴交于两点A(x1,0)、B(x2,0)且0<x1<x2.求证:g′(px1+qx2)<0(其中正常数p,q满足p+q=1,且q≥p).
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:综合题
分析:(1)由f(x)+m=0可化为f(x)=-m,即求一个函数值对应两个自变量.由图象可知要求函数的极值与端点函数值.因此先求出f′(x),在区间[
,e]内判定f(x)的单调性并求极值.从图象中确定-m的取值范围,进一步确定m的取值范围.
(2)先对g(x)求导,发现表达式中含x,a;结合题要求消去a.化简g′(px1+qx2),通过放缩法和换元法证明不等式成立.
| 1 |
| e |
(2)先对g(x)求导,发现表达式中含x,a;结合题要求消去a.化简g′(px1+qx2),通过放缩法和换元法证明不等式成立.
解答:
解:(1)由f(x)=2lnx-x2求导得到:
f′(x)=
,
∵x∈
,e],故f′(x)在x=1有唯一的极值点,f(
)=-2-
,
f(e)=-2-e2,f(x)极大值=f(1)=-1,
且知f(e)<f(
),故f(x)=-m在[
,e]内有两个不等的实根满足:-2-
≤-m<-1
故m的取值范围为(1,2+
].
(2)g′(x)=
-2x-a,又f(x)-ax=0有两个不同的实根x1、x2,则
则a=
-(x1+x2)
于是g′(px1+qx2)=
-2(px1+qx2)-[
-(x1+x2)]
=
-
+(2p-1)(x2-x1)
∵2p≤1,0<x1<x2,∴(2p-1)(x2-x1)≤0
要证:g′(px1+qx2)<0,只需证:
+
<0
即证:
+ln
<0①
令
=t,0<t<1,即证:u(t)=
+lnt<0在0<t<1上恒成立,
又u′(t)=
-
=
∵正常数p,q,p+q=1,且q≥p,则
≥1.
可知:t-1<0,t-
<0,
故知u′(t)>0∴u(t)在t∈(0,1)上为增函数,
则u(t)<u(1)=0,从而知①成立,从而原不等式成立.
f′(x)=
| 2(1-x)(1+x) |
| x |
∵x∈
| 1 |
| e |
| 1 |
| e |
| 1 |
| e2 |
f(e)=-2-e2,f(x)极大值=f(1)=-1,
且知f(e)<f(
| 1 |
| e |
| 1 |
| e |
| 1 |
| e2 |
故m的取值范围为(1,2+
| 1 |
| e2 |
(2)g′(x)=
| 2 |
| x |
|
则a=
| 2(lnx1-lnx2) |
| x1-x2 |
于是g′(px1+qx2)=
| 2 |
| px1+qx2 |
| 2(lnx1-lnx2) |
| x1-x2 |
=
| 2 |
| px1+qx2 |
| 2(lnx1-lnx2) |
| x1-x2 |
∵2p≤1,0<x1<x2,∴(2p-1)(x2-x1)≤0
要证:g′(px1+qx2)<0,只需证:
| 2 |
| px1+qx2 |
| 2(lnx1-lnx2) |
| x2-x1 |
即证:
| x2-x1 |
| px1+qx2 |
| x1 |
| x2 |
令
| x1 |
| x2 |
| 1-t |
| pt+q |
又u′(t)=
| 1 |
| t |
| 1 |
| (pt+q)2 |
p2(t-1)(t-
| ||
| t(pt+q)2 |
∵正常数p,q,p+q=1,且q≥p,则
| q2 |
| p2 |
可知:t-1<0,t-
| q2 |
| p2 |
故知u′(t)>0∴u(t)在t∈(0,1)上为增函数,
则u(t)<u(1)=0,从而知①成立,从而原不等式成立.
点评:考查学生会利用导数确定图象的大致形状,并在此基础上在题目条件要求下确定函数值的取值范围;同时应用了转化的思想.第二问考查了学生消参的方法、及通过放缩法,换元法证明不等式的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
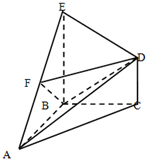 如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: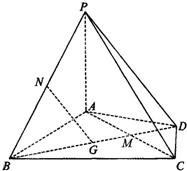 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且