题目内容
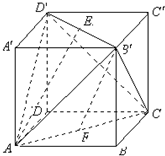 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:(1)直线AB′和平面ACD′所成角的正弦值;
(2)二面角B′-CD′-A的余弦值;
(3)点B到平面ACD′的距离.
考点:点、线、面间的距离计算,与二面角有关的立体几何综合题
专题:计算题,空间位置关系与距离
分析:(1)建立空间直角坐标系,求出平面ACD'的一个法向量,利用向量的夹角公式,即可求直线AB′和平面ACD′所成角的正弦值;
(2)求出平面B'CD'的一个法向量,利用向量的夹角公式,即可求二面角B′-CD′-A的余弦值;
(3)点B到平面ACD'的距离d=|
|=
.
(2)求出平面B'CD'的一个法向量,利用向量的夹角公式,即可求二面角B′-CD′-A的余弦值;
(3)点B到平面ACD'的距离d=|
| ||||
|
|
| 2 |
| 3 |
| 3 |
解答:
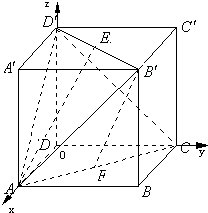 解:如图建立空间直角坐标系O-xyz,
解:如图建立空间直角坐标系O-xyz,
∵正方体的棱长等于2,E,F分别是B'D',AC的中点,
∴A(2,0,0),B(2,2,0),C(0,2,0),D'(0,0,2),B'(2,2,2),E(1,1,2),F(1,1,0).
(1)
=(-2,0,2),
=(-2,2,0),
=(0,2,2),
设
=(x′,y′,z′)是平面ACD'的一个法向量,则
由
⇒
⇒
,
取x'=1,得平面ACD'的一个法向量
=(1,1,1),
设直线AB'和平面ACD'所成角的大小为θ,则sinθ=|
|=|
|=
∴直线AB'和平面ACD'所成角的正弦值是
(2)
=(2,2,0),
=(0,2,-2),
设
=(x0,y0,z0)是平面B'CD'的一个法向量,则
由
得
,取y0=1得平面B'CD'的一个法向量
=(-1,1,1)
由cosθ=
=
=
,
故二面角B'-CD'-A的余弦值是
(3)∵
=(-2,-2,2),平面ACD'的一个法向量
=(1,1,1),
∴点B到平面ACD'的距离d=|
|=
 解:如图建立空间直角坐标系O-xyz,
解:如图建立空间直角坐标系O-xyz,∵正方体的棱长等于2,E,F分别是B'D',AC的中点,
∴A(2,0,0),B(2,2,0),C(0,2,0),D'(0,0,2),B'(2,2,2),E(1,1,2),F(1,1,0).
(1)
| AD′ |
| AC |
| AB′ |
设
| n |
由
|
|
|
取x'=1,得平面ACD'的一个法向量
| n |
设直线AB'和平面ACD'所成角的大小为θ,则sinθ=|
| ||||
|
|
| (1,1,1)•(0,2,2) | ||||
|
| ||
| 3 |
∴直线AB'和平面ACD'所成角的正弦值是
| ||
| 3 |
(2)
| D′B′ |
| D′C |
设
| m |
由
|
|
| m |
由cosθ=
| ||||
|
|
| (1,1,1)•(-1,1,1) | ||||
|
| 1 |
| 3 |
故二面角B'-CD'-A的余弦值是
| 1 |
| 3 |
(3)∵
| BD′ |
| n |
∴点B到平面ACD'的距离d=|
| ||||
|
|
| 2 |
| 3 |
| 3 |
点评:本题考查空间向量的运用,考查线面角,面面角,考查点到面的距离,考查学生的计算能力,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在一个三角形的三边长之比为3:5:7,则其最大的角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在Rt△AOB中,
在Rt△AOB中,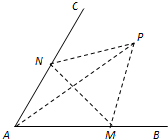 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.