题目内容
已知函数f（x）=2sin（2x-
），x∈R，
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的单调区间．
| π |
| 3 |
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的单调区间．
考点：正弦函数的单调性,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（1）根据三角函数的周期公式，即可得到结论．
（2）根据三角函数的单调性的性质即可得到结论．
（2）根据三角函数的单调性的性质即可得到结论．
解答：
解：（1）根据三角函数的周期公式可得周期T=
=π．
（2）解：由-
+2kπ≤2x-
≤
+2kπ，
解得kπ-
≤x≤kπ+
，k∈Z，
故函数的单调递增区间为[kπ-
，kπ+
]，k∈Z，
由
+2kπ≤2x-
≤
+2kπ，
解得kπ+
≤x≤kπ+
，k∈Z，
故函数的单调递减区间为[kπ+
，kπ+
]，k∈Z．
| 2π |
| 2 |
（2）解：由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得kπ-
| π |
| 12 |
| 5π |
| 12 |
故函数的单调递增区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
由
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得kπ+
| 5π |
| 12 |
| 11π |
| 12 |
故函数的单调递减区间为[kπ+
| 5π |
| 12 |
| 11π |
| 12 |
点评：本题主要考查函数单调区间的求解，利用正弦函数的图象和性质是解决本题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
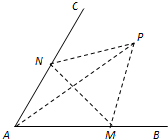如图，经过村庄A有两条夹角为60°的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M、N （异于村庄A），要求PM=PN=MN=2（单位：千米）．设∠AMN=θ．
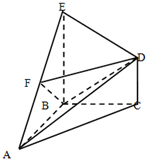如图，在几何体ABCDE中，BE⊥平面ABC，CD∥BE，△ABC是等腰直角三角形，∠ABC=90°，且BE=AB=2，CD=1，点F是AE的中点．建立适当的空间直角坐标系，利用空间向量方法解答以下问题：