题目内容
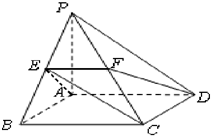 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.(1)求证:PB⊥平面AEFD;
(2)求直线EC与平面PAD所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由PA⊥平面ABCD,得AD⊥PA,结合AD⊥AB,得AD⊥平面PAB,从而AD⊥PB,最后根据△PAB中,中线AE⊥PB且AE、AD是平面AEFD内的相交直线,证出PB⊥平面AEFD;
(2)取PA中点G,CD中点H,连接EG、GH、GD,证明∠HGD即为直线EC与平面PAD所成的角,求出GH,即可求出直线EC与平面PAD所成角的正弦值.
(2)取PA中点G,CD中点H,连接EG、GH、GD,证明∠HGD即为直线EC与平面PAD所成的角,求出GH,即可求出直线EC与平面PAD所成角的正弦值.
解答:
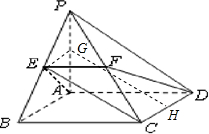 (1)证明:∵PA⊥平面ABCD,底面ABCD是矩形
(1)证明:∵PA⊥平面ABCD,底面ABCD是矩形
∴AD⊥平面PAB,∴AD⊥PB
∵E是PB的中点,AB=AP,∴AE⊥PB
∵AB∩AE=A,
∴PB⊥平面AEFD…(6分)
(2)解:∵PA⊥平面ABCD,∴CD⊥PA,
又CD⊥AD,∴CD⊥平面PAD,…(8分)
取PA中点G,CD中点H,连接EG、GH、GD,
则EG∥AB∥CD且EG=
AB=1,
∴EGHC是平行四边形,∴EC∥HG
∴∠HGD即为直线EC与平面PAD所成的角…(12分)
在Rt△GAD中,GH=
,sin∠HGD=
=
=
,
∴直线EC与平面PAD所成角的正弦值为
…(14分)
 (1)证明:∵PA⊥平面ABCD,底面ABCD是矩形
(1)证明:∵PA⊥平面ABCD,底面ABCD是矩形∴AD⊥平面PAB,∴AD⊥PB
∵E是PB的中点,AB=AP,∴AE⊥PB
∵AB∩AE=A,
∴PB⊥平面AEFD…(6分)
(2)解:∵PA⊥平面ABCD,∴CD⊥PA,
又CD⊥AD,∴CD⊥平面PAD,…(8分)
取PA中点G,CD中点H,连接EG、GH、GD,
则EG∥AB∥CD且EG=
| 1 |
| 2 |
∴EGHC是平行四边形,∴EC∥HG
∴∠HGD即为直线EC与平面PAD所成的角…(12分)
在Rt△GAD中,GH=
| 18 |
| HD |
| GH |
| 1 | ||
|
| ||
| 6 |
∴直线EC与平面PAD所成角的正弦值为
| ||
| 6 |
点评:本题在四棱锥中,证明了线面垂直并求直线与平面所成角的正弦之值,着重考查了直线与平面垂直的判定与性质等知识,属于中档题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 对一根作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.
对一根作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.