题目内容
已知函数f(x)=x+
,x∈[1,+∞),a>0.
(1)当a=
时,求函数f(x)的最小值;
(2)若函数f(x)的最小值为4,求实数a.
| a |
| x |
(1)当a=
| 1 |
| 2 |
(2)若函数f(x)的最小值为4,求实数a.
考点:基本不等式
专题:导数的综合应用,不等式的解法及应用
分析:(1)利用导数研究函数f(x)的单调性即可得出;
(2)通过对a分类讨论,利用导数研究函数f(x)的单调性即可得出.
(2)通过对a分类讨论,利用导数研究函数f(x)的单调性即可得出.
解答:
解(1)a=
时,f(x)=x+
,x∈[1,+∞),
∴f′(x)=1-
=
,
当x≥1时,f′(x)>0,
∴函数f(x)在x∈[1,+∞)单调递增,
∴当x=1时,函数f(x)取得最小值f(1),且f(1)=1+
=
.
(2)f′(x)=1-
=
=
,
①当a>1时,
当x>
时,f′(x)>0,此时函数f(x)单调递增;当1<x<
时,f′(x)<0,此时函数f(x)单调递减.
∴当x=
时,函数f(x)取得极小值即最小值f(
)=
+
=2
=4,解得a=4>1,因此a=4适合.
②当0<a≤1时,f′(x)≥0,此时函数f(x)在[1,+∞)上单调递增,
∴当x=1时,f(x)取得最小值,f(1)=1+a=4,解得a=3>1,不满足条件,应舍去.
综上可得:a=4.
| 1 |
| 2 |
| 1 |
| 2x |
∴f′(x)=1-
| 1 |
| 2x2 |
(
| ||||
| 2x2 |
当x≥1时,f′(x)>0,
∴函数f(x)在x∈[1,+∞)单调递增,
∴当x=1时,函数f(x)取得最小值f(1),且f(1)=1+
| 1 |
| 2 |
| 3 |
| 2 |
(2)f′(x)=1-
| a |
| x2 |
| x2-a |
| x2 |
(x+
| ||||
| x2 |
①当a>1时,
当x>
| a |
| a |
∴当x=
| a |
| a |
| a |
| a | ||
|
| a |
②当0<a≤1时,f′(x)≥0,此时函数f(x)在[1,+∞)上单调递增,
∴当x=1时,f(x)取得最小值,f(1)=1+a=4,解得a=3>1,不满足条件,应舍去.
综上可得:a=4.
点评:本题考查了利用导数研究函数的单调性极值最值的方法,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
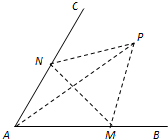 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.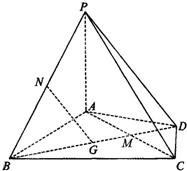 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且