题目内容
已知双曲线C的焦点F(
,0),双曲线C上一点P到F的最短距离为
-
.
(1)求双曲线的标准方程和渐近线方程;
(2)已知点M(0,1),设P是双曲线C上的点,Q是点P关于原点的对称点:设λ=
•
,求λ的取值范围.
| 3 |
| 3 |
| 2 |
(1)求双曲线的标准方程和渐近线方程;
(2)已知点M(0,1),设P是双曲线C上的点,Q是点P关于原点的对称点:设λ=
| MP |
| MQ |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意知c,a再根据b2=c2-a2,问题得以解决,再令双曲线方程的右边为0,化简即可得到双曲线的渐近线方程;
(2)用坐标表示向量,利用向量的数量积建立函数关系式,根据双曲线的范围,可求得λ的取值范围.
(2)用坐标表示向量,利用向量的数量积建立函数关系式,根据双曲线的范围,可求得λ的取值范围.
解答:
解:(1)∵双曲线C的焦点F(
,0),双曲线C上一点P到F的最短距离为
-
.
可设双曲线的方程为
-
=1,
∴c=
,c-a=
-
,
∴a=
,
∴b2=c2-a2=(
)2-(
)2=1,
则双曲线的方程为:
-y2=1,
令
-y2=0,
则y=±
x,
即渐近线方程为y=±
x;
(2)设P的坐标为(x0,y0),则Q的坐标为(-x0,-y0),
∴λ=
•
=(x0,y0-1)•(-x0,-y0-1)=-x02-y02+1=-
x02+2
∵|x0|≥
∴λ的取值范围是(-∞,-1].
| 3 |
| 3 |
| 2 |
可设双曲线的方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴c=
| 3 |
| 3 |
| 2 |
∴a=
| 2 |
∴b2=c2-a2=(
| 3 |
| 2 |
则双曲线的方程为:
| x2 |
| 2 |
令
| x2 |
| 2 |
则y=±
| ||
| 2 |
即渐近线方程为y=±
| ||
| 2 |
(2)设P的坐标为(x0,y0),则Q的坐标为(-x0,-y0),
∴λ=
| MP |
| MQ |
| 3 |
| 2 |
∵|x0|≥
| 2 |
∴λ的取值范围是(-∞,-1].
点评:本题以双曲线为载体,考查双曲线的几何性质,考查向量的数量积,考查函数的值域,属于中档题.

练习册系列答案
相关题目
设a>b>c,k∈R,且(a-c)•(
+
)≥k恒成立,则k的最大值为( )
| 1 |
| a-b |
| 1 |
| b-c |
| A、2 | B、3 | C、4 | D、5 |
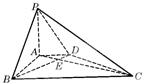 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2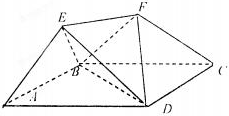 如图,底面ABCD是边长为2的菱形,且∠BAD=
如图,底面ABCD是边长为2的菱形,且∠BAD=