题目内容
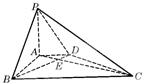 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2| 3 |
(Ⅰ)求证:BD⊥平面PAC
(Ⅱ)求二面角P-BD-A的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)分别在Rt△ABD和Rt△ABC求得tan∠ABD和tan∠BAC的值,分别求得∠ABD和∠ABC,进而求得∠AEB=90,推断出AC⊥BD,进而根据线面垂直的性质和PA⊥平面ABCD推断出PA⊥BD,最后根据线面垂直的判定定理推断出BD⊥平面PAC.
(Ⅱ)连结PE,由PA⊥平面ABCD,AE⊥BD,推断出PE⊥BD,进而可知∠PEA为二面角P-BD-A的平面角,Rt△ABE中求得AE,进而在Rt△APE中求得tan∠AEP,则∠AEP可求.
(Ⅱ)连结PE,由PA⊥平面ABCD,AE⊥BD,推断出PE⊥BD,进而可知∠PEA为二面角P-BD-A的平面角,Rt△ABE中求得AE,进而在Rt△APE中求得tan∠AEP,则∠AEP可求.
解答:
(Ⅰ)证明:在Rt△ABD中,tan∠ABD=
=
,
∴∠ABD=30°,
在Rt△ABC中,tan∠BAC=
=
,
∴∠ABC=60°,
∴∠AEB=180°-∠ABC-∠ABD=90°,即AC⊥BD,
∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵AC∩AP=A,AC?平面APC,AP?平面APC,
∴BD⊥平面PAC
(Ⅱ)连结PE,∵PA⊥平面ABCD,AE⊥BD,
∴PE⊥BD,即∠PEA为二面角P-BD-A的平面角,
在Rt△ABE中,∠ABE=30°,
∴AE=
AB=
,
在Rt△APE中,tan∠AEP=
=
=
,
∴∠AEP=arctan
.
| AD |
| AB |
| ||
| 3 |
∴∠ABD=30°,
在Rt△ABC中,tan∠BAC=
| BC |
| AB |
| 3 |
∴∠ABC=60°,
∴∠AEB=180°-∠ABC-∠ABD=90°,即AC⊥BD,
∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵AC∩AP=A,AC?平面APC,AP?平面APC,
∴BD⊥平面PAC
(Ⅱ)连结PE,∵PA⊥平面ABCD,AE⊥BD,
∴PE⊥BD,即∠PEA为二面角P-BD-A的平面角,
在Rt△ABE中,∠ABE=30°,
∴AE=
| 1 |
| 2 |
| 3 |
在Rt△APE中,tan∠AEP=
| AP |
| AE |
| 4 | ||
|
4
| ||
| 3 |
∴∠AEP=arctan
4
| ||
| 3 |
点评:本题主要考查了线面垂直的判定定理的应用,二面角的计算.解题的关键是找到二面角的平面角.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
设f(x)=
,若
f(x)存在,则常数b的值是( )
|
| lim |
| x→0 |
| A、0 | B、1 | C、-1 | D、e |
下列函数中,以为π最小正周期的偶函数,且在(0,
)内递增的是( )
| π |
| 2 |
| A、y=sin|x| |
| B、y=|sinx| |
| C、y=|cosx| |
| D、y=cos|x| |