题目内容
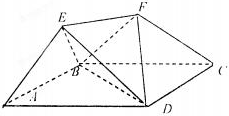 如图,底面ABCD是边长为2的菱形,且∠BAD=
如图,底面ABCD是边长为2的菱形,且∠BAD=| π |
| 3 |
| π |
| 2 |
(1)求证:EF∥平面ABCD;
(2)求多面体ABCDEF的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)作EO1⊥面ABCD于O1,作FO2⊥面ABCD于O2,证明O1O2∥EF,利用直线与平面平行的判定定理证明EF∥平面ABCD.
(2)取BD中点为O,联接EO,OF,得到BD⊥平面EOF,多面体ABCDEF的体积VABCDEF=VE-ABD+VF-CBD+VB-EFD求解即可.
(2)取BD中点为O,联接EO,OF,得到BD⊥平面EOF,多面体ABCDEF的体积VABCDEF=VE-ABD+VF-CBD+VB-EFD求解即可.
解答:
 解:(1)作EO1⊥面ABCD于O1,作FO2⊥面ABCD于O2,
解:(1)作EO1⊥面ABCD于O1,作FO2⊥面ABCD于O2,
因E-ABD与F-CBD都是正三棱锥,
且O1、O2分别为△ABD与△CBD的中心,
∴EO1∥FO2,且
EO1=FO2=
.…(3分)
所以四边形EO1O2F是平行四边形,所以O1O2∥EF.…(4分)
又O1O2?面ABCD,EF?平面ABCD,所以EF∥平面ABCD.…(6分)
(2)又O1O2⊥DB,则BD⊥平面EO1O2F,故FO2⊥DB.…(8分)
取BD中点为O,联接EO,OF即BD⊥平面EOF,
易算出VB=EFD=
S△EOF•|BD|=
×(
×
×
)×2=
…(10分)
VE-ABD=VF-CBD=
×(
×
×
)×
=
…(11分)
多面体ABCDEF的体积VABCDEF=VE-ABD+VF-CBD+VB-EFD=2×
+
=
…(13分)
 解:(1)作EO1⊥面ABCD于O1,作FO2⊥面ABCD于O2,
解:(1)作EO1⊥面ABCD于O1,作FO2⊥面ABCD于O2,因E-ABD与F-CBD都是正三棱锥,
且O1、O2分别为△ABD与△CBD的中心,
∴EO1∥FO2,且
EO1=FO2=
| ||
| 3 |
所以四边形EO1O2F是平行四边形,所以O1O2∥EF.…(4分)
又O1O2?面ABCD,EF?平面ABCD,所以EF∥平面ABCD.…(6分)
(2)又O1O2⊥DB,则BD⊥平面EO1O2F,故FO2⊥DB.…(8分)
取BD中点为O,联接EO,OF即BD⊥平面EOF,
易算出VB=EFD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 9 |
VE-ABD=VF-CBD=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 3 |
多面体ABCDEF的体积VABCDEF=VE-ABD+VF-CBD+VB-EFD=2×
| ||
| 3 |
2
| ||
| 9 |
8
| ||
| 9 |
点评:本题考查直线与平面平行的判定定理的应用,多面体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,以为π最小正周期的偶函数,且在(0,
)内递增的是( )
| π |
| 2 |
| A、y=sin|x| |
| B、y=|sinx| |
| C、y=|cosx| |
| D、y=cos|x| |
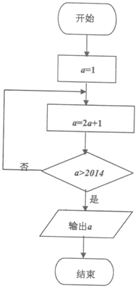 根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….
根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….