题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
=0相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足
+
=t
(其中O为坐标原点),求整数t的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足
| OA |
| OB |
| OP |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件得e=
=
,b=
=1,由此能求出椭圆C的方程.
(Ⅱ)设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由
得(1+2k2)x2-8k2x+8k2-2=0,由此利用根的判别式和韦达定理结合已知条件能求出t的最大整数值.
| c |
| a |
| ||
| 2 |
| ||
|
(Ⅱ)设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由
|
解答:
解:(Ⅰ)由题知e=
=
,
∴e2=
=
=
.即a2=2b2.
又∴b=
=1,
∴a2=2,b2=1.
∴椭圆C的方程为
+y2=1.…(5分)
(Ⅱ)由题意知直线AB的斜率存在.
设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由
得(1+2k2)x2-8k2x+8k2-2=0.
△=64k4-4(2k2+1)(8k2-2)>0,
k2<
.x1+x2=
,x1x2=
…(8分)
∵
+
=t
,
∴(x1+x2,y1+y2)=t(x,y),
x=
=
,y=
=
[k(x1+x2)-4k]=
.
∵点P在椭圆上,∴
+2
=2,
∴16k2=t2(1+2k2)…(12分)
t2=
=
<
=4,则-2<t<2,
∴t的最大整数值为1.…(14分)
| c |
| a |
| ||
| 2 |
∴e2=
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
又∴b=
| ||
|
∴a2=2,b2=1.
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)由题意知直线AB的斜率存在.
设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由
|
△=64k4-4(2k2+1)(8k2-2)>0,
k2<
| 1 |
| 2 |
| 8k2 |
| 1+2k2 |
| 8k2-2 |
| 1+2k2 |
∵
| OA |
| OB |
| OP |
∴(x1+x2,y1+y2)=t(x,y),
x=
| x1+x2 |
| t |
| 8k2 |
| t(1+2k2) |
| y1+y2 |
| t |
| 1 |
| t |
| -4k |
| t(1+2k2) |
∵点P在椭圆上,∴
| (8k2)2 |
| t2(1+2k2)2 |
| (-4k)2 |
| t2(1+2k2)2 |
∴16k2=t2(1+2k2)…(12分)
t2=
| 16k2 |
| 1+2k2 |
| 16 | ||
|
| 16 |
| 2+2 |
∴t的最大整数值为1.…(14分)
点评:本题考查椭圆方程的求法,考查整数的最大值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
因为无理数是无限小数,而π是无理数,所以π是无限小数.属于哪种推理( )
| A、合情推理 | B、演绎推理 |
| C、类比推理 | D、归纳推理 |
下列函数中,以为π最小正周期的偶函数,且在(0,
)内递增的是( )
| π |
| 2 |
| A、y=sin|x| |
| B、y=|sinx| |
| C、y=|cosx| |
| D、y=cos|x| |
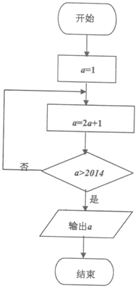 根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….
根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….