题目内容
已知
=(λcosα,λsinα)(λ≠0),
=(-sinβ,cosβ),其中O为坐标原点.
(1)若∠B=α-30°,求
和
的夹角;
(2)若|
|≥|
|,对于任意实数α、β都成立,求实数λ的取值范围.
| OA |
| OB |
(1)若∠B=α-30°,求
| OA |
| OB |
(2)若|
| AB |
| OB |
考点:平面向量数量积的运算
专题:计算题,不等式的解法及应用,平面向量及应用
分析:(1)设向量
与
的夹角为θ,由
•
=|
|•|
|cosθ=|λ|cosθ=λcosα(-sinβ)+(λsinα)cosβ=λsin(α-β)=λsin30°=
λ,可求夹角;
(2)|
|2=|
-
|2=|
|2-2
•
+|
|2=λ2-2λsin(α-β)+1,不等式|
|≥|
|可化为λ2-2λsin(α-β)≥0对任意实数α、β都成立,则有
;
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| 1 |
| 2 |
(2)|
| AB |
| OA |
| OB |
| OA |
| OA |
| OB |
| OB |
| AB |
| OB |
|
解答:
(1)
=(λcosα,λsinα),
=(-sinβ,cosβ),
∴|
|=|λ|,|
|=1,
设向量
与
的夹角为θ,得
•
=|
|•|
|cosθ=|λ|cosθ,
又∵
•
=λcosα(-sinβ)+(λsinα)cosβ=λsin(α-β)=λsin30°=
λ,
∴cosθ=±
,
∵0°≤θ≤180°,
∴θ=60°或120°;
(2)|
|2=|
-
|2=|
|2-2
•
+|
|2=λ2-2λsin(α-β)+1,
不等式|
|≥|
|可化为:λ2-2λsin(α-β)+1≥1,即λ2-2λsin(α-β)≥0对任意实数α、β都成立,
∵-1≤sin(α-β)≤1,
∴
,解得:λ≤-2或λ≥2,
∴实数λ的取值范围是(-∞,-2]∪[2,+∞).
| OA |
| OB |
∴|
| OA |
| OB |
设向量
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
又∵
| OA |
| OB |
| 1 |
| 2 |
∴cosθ=±
| 1 |
| 2 |
∵0°≤θ≤180°,
∴θ=60°或120°;
(2)|
| AB |
| OA |
| OB |
| OA |
| OA |
| OB |
| OB |
不等式|
| AB |
| OB |
∵-1≤sin(α-β)≤1,
∴
|
∴实数λ的取值范围是(-∞,-2]∪[2,+∞).
点评:该题考查平面向量数量积运算、向量夹角公式,考查恒成立问题,考查不等式的求解等知识.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
因为无理数是无限小数,而π是无理数,所以π是无限小数.属于哪种推理( )
| A、合情推理 | B、演绎推理 |
| C、类比推理 | D、归纳推理 |
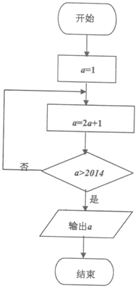 根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….
根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….