题目内容
直线L1，L2都过点（1，-2）且互相垂直，若抛物线y=ax2与两直线中至少一条相交，求a的取值范围．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意直线l1，l2的斜率分别设为k1，k2，过点P（1，-2）的直线设为y=k（x-1）-2，由由y=k（x-1）-2与抛物线y=ax2联立，得ax2-kx+k+2=0，由直线l1、l2都过点P（1，-2）且都与抛物线相切，知a≠0，△=k2-4ak-8a≥0，再由l1⊥l2，能求出a的取值范围．
解答：
解：由题意直线L1，L2的斜率，分别设为k1，k2，
过点P（1，-2）的直线设为y=k（x-1）-2，
由y=k（x-1）-2与抛物线y=ax2联立，得ax2-kx+k+2=0，
∵抛物线y=ax2与两直线中至少一条相交，
∴a≠0，△=k2-4ak-8a≥0
∵l1⊥l2，
∴k1k2=
=-1，
∴k=-a-2，
∴（-a-2）2-4（-a-2）a-8a≥0，
∴5a2+4a+4≥0，恒成立
斜率不存在时，同样成立．
∴a≠0．
过点P（1，-2）的直线设为y=k（x-1）-2，
由y=k（x-1）-2与抛物线y=ax2联立，得ax2-kx+k+2=0，
∵抛物线y=ax2与两直线中至少一条相交，
∴a≠0，△=k2-4ak-8a≥0
∵l1⊥l2，
∴k1k2=
| k+2 |
| a |
∴k=-a-2，
∴（-a-2）2-4（-a-2）a-8a≥0，
∴5a2+4a+4≥0，恒成立
斜率不存在时，同样成立．
∴a≠0．
点评：通过几何量的转化考查用待定系数法求曲线方程的能力，通过直线与圆锥曲线的位置关系处理，考查学生的运算能力．通过向量与几何问题的综合，考查学生分析转化问题的能力，探究研究问题的能力，并体现了合理消元，设而不解的代数变形的思想．
练习册系列答案
相关题目
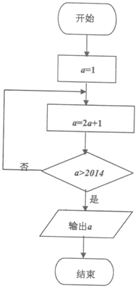根据如图所示的程序框图，变量a每次赋值后的结果依次记作：a1、a2、a3…an…．如a1=1，a2=3…．
把正整数按一定的规则排成了如图所示的三角形数表．