题目内容
已知非零向量
，
，
满足
+
+
=0，向量
，
的夹角为120°，且|
|=2|
|，求向量
与
的夹角．
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| a |
| c |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：解：由题意可画出右边的图示，在平行四边形OABC中，由条件求得∠AOB=30°，即AB⊥OB，可得向量
与
的夹角．
| a |
| c |
解答：
解：由题意可画出右边的图示，在平行四边形OABC中，
因为∠OAB=60°，|
|=2|
|，
所以∠AOB=30°，即AB⊥OB，
即向量
与
的夹角为90°．
解：由题意可画出右边的图示，在平行四边形OABC中，因为∠OAB=60°，|
| b |
| a |
所以∠AOB=30°，即AB⊥OB，
即向量
| a |
| c |
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，体现了数形结合的数学思想，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
240°化成弧度制是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
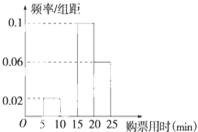某车站在春运期间为了了解旅客购票情况，随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t（以下简称为购票用时，单位为min），如图是这次调查统计分析得到的数据（如图所示）．