题目内容
15.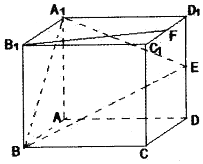 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.(1)求三棱锥B1-A1BE的体积;
(2)试判断直线B1F与平面A1BE是否平行,如果平行,请在平面A1BE上作出与B1F平行的直线,并说明理由.
分析 (1)三棱锥B1-A1BE的体积${V_{{B_1}-{A_1}BE}}={V_{E-{A_1}{B_1}B}}=\frac{1}{3}{S_{△{A_1}{B_1}B}}•DA$,由此能求出结果.
(2)B1F∥平面A1BE,延长A1E交AD延长线于H,连BH交CD于G点,则BG就是在平面A1BE上与B1F平行的直线.
解答 解:(1)如图所示,
∵在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.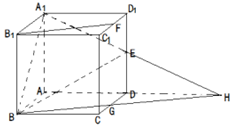
∴三棱锥B1-A1BE的体积:
${V_{{B_1}-{A_1}BE}}={V_{E-{A_1}{B_1}B}}=\frac{1}{3}{S_{△{A_1}{B_1}B}}•DA=\frac{1}{3}•\frac{1}{2}•2•2•2=\frac{4}{3}$.
(2)B1F∥平面A1BE.
延长A1E交AD延长线于H,连BH交CD于G点,
则BG就是在平面A1BE上与B1F平行的直线.
证明如下:
因为BA1∥平面CDD1C1,平面A1BH∩平面CDD1C1=GE,
所以A1B∥GE,又A1B∥CD1,则G为CD的中点,
故BG∥B1F,BG就是在平面A1BE上与B1F平行的直线.
点评 本题考查三棱锥的体积的求法,考查线面是否平行的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,右焦点为F(c,0),弦PQ过F且垂直于x轴,过点P、点Q分别作直线AQ、AP的垂线,两垂线交于点B,若B到直线PQ的距离小于2(a+c),则该双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
10.设某几何体的三视图如图所示,则该几何体的体积为( )
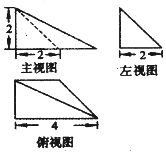

| A. | 8 | B. | 4 | C. | 2 | D. | $\frac{4}{3}$ |
7.如果复数$\frac{2+ai}{1+2i}$的实部与虚部相等,则实数a等于( )
| A. | $\frac{2}{3}$ | B. | 6 | C. | -6 | D. | -$\frac{2}{3}$ |
4.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$\sqrt{3}$,AB=2$\sqrt{2},AC=\sqrt{2},∠BAC={60°}$,则此球的体积等于( )
| A. | $\frac{{8\sqrt{2}π}}{3}$ | B. | $\frac{9π}{2}$ | C. | $\frac{{5\sqrt{10}π}}{3}$ | D. | $\frac{{4\sqrt{3}π}}{3}$ |
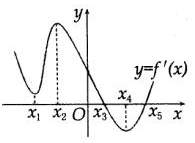 如图是函数y=f(x)的导函数y=f′(x)的图象,下列关于函数y=f(x)的极值和单调性的说法中,正确的个数是( )
如图是函数y=f(x)的导函数y=f′(x)的图象,下列关于函数y=f(x)的极值和单调性的说法中,正确的个数是( )