题目内容
10.设某几何体的三视图如图所示,则该几何体的体积为( )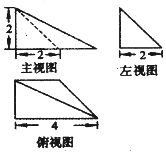
| A. | 8 | B. | 4 | C. | 2 | D. | $\frac{4}{3}$ |
分析 几何体是一个四棱锥,四棱锥的底面是一个直角梯形,直角梯形的上底是2,下底是4,垂直于底边的腰是2,一条侧棱与底面垂直,这条侧棱长是2,即可求出几何体的体积.
解答 解:由三视图知,几何体是一个四棱锥,四棱锥的底面是一个直角梯形,
直角梯形的上底是2,下底是4,垂直于底边的腰是2,
一条侧棱与底面垂直,这条侧棱长是2,
∴四棱锥的体积是$\frac{1}{3}•\frac{(2+4)×2}{2}×2$=4,
故选B.
点评 本题考查由三视图求几何体的体积,在三个图形中,俯视图确定锥体的名称,即是几棱锥,正视图和侧视图确定锥体的高,注意高的大小.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
18.《九章算术》教会了人们用等差数列的知识来解决问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织( )尺布.
| A. | $\frac{1}{2}$ | B. | $\frac{24}{29}$ | C. | $\frac{16}{31}$ | D. | $\frac{16}{29}$ |
11.已知命题q:?x∈R,cosx≤1,则¬q是( )
| A. | ?x∈R,cosx≥1 | B. | ?x∈R,cosx>1 | C. | ?x0∈R,cosx0≥1 | D. | ?x0∈R,cosx0>1 |
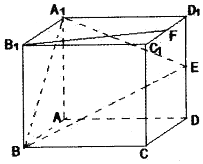 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.