题目内容
4.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$\sqrt{3}$,AB=2$\sqrt{2},AC=\sqrt{2},∠BAC={60°}$,则此球的体积等于( )| A. | $\frac{{8\sqrt{2}π}}{3}$ | B. | $\frac{9π}{2}$ | C. | $\frac{{5\sqrt{10}π}}{3}$ | D. | $\frac{{4\sqrt{3}π}}{3}$ |
分析 画出球的内接三棱柱ABC-A1B1C1,作出球的半径,然后可求球的表面积.
解答  解:设AA1=h,则
解:设AA1=h,则
∵棱柱的体积为$\sqrt{3}$,AB=2$\sqrt{2},AC=\sqrt{2},∠BAC={60°}$,
∴$\frac{1}{2}×2\sqrt{2}×\sqrt{2}×\frac{\sqrt{3}}{2}h=\sqrt{3}$
∴h=1,
∵AB=2$\sqrt{2},AC=\sqrt{2},∠BAC={60°}$,
∴BC=$\sqrt{8+2-2×2\sqrt{2}×\sqrt{2}×\frac{1}{2}}$=$\sqrt{6}$,
如图,连接上下底面外心,O为PQ的中点,OP⊥平面ABC,
AP=$\frac{\sqrt{6}}{2×\frac{\sqrt{3}}{2}}$=$\sqrt{2}$
则球的半径为OA,
由题意OP=$\frac{1}{2}$,∴OA=$\sqrt{\frac{1}{4}+2}$=$\frac{3}{2}$,
所以球的体积为:$\frac{4}{3}$πR3=$\frac{9}{2}$π
故选B.
点评 本题是基础题,解题思路是:先求底面外接圆的半径,转化为直角三角形,求出球的半径,这是三棱柱外接球的常用方法;本题考查空间想象能力,计算能力.

练习册系列答案
相关题目
9.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y+6≥0}\\{x≤3}\\{x+y+k≥0}\end{array}\right.$,且z=2x+4y的最小值为2,则常数k=( )
| A. | 2 | B. | -2 | C. | 6 | D. | 3 |
4.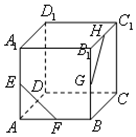 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
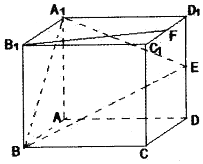 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点. 在直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.