题目内容
7.如果复数$\frac{2+ai}{1+2i}$的实部与虚部相等,则实数a等于( )| A. | $\frac{2}{3}$ | B. | 6 | C. | -6 | D. | -$\frac{2}{3}$ |
分析 利用复数的运算法则、共轭复数的定义、实部、虚部即可得出.
解答 解:∵复数$\frac{2+ai}{1+2i}$=$\frac{(2+ai)(1-2i)}{(1+2i)(1-2i)}$=$\frac{2+2a}{5}$+$\frac{(a-4)}{5}$i的实部与虚部相等,
∴$\frac{2+2a}{5}$=$\frac{(a-4)}{5}$,解得a=-6,
故选:C.
点评 本题考查了复数的运算法则、共轭复数的定义、实部与虚部的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.某学校为了解该校高三年级学生数学科学习情况,对广一模考试数学成绩进行分析,从中抽取了n 名学生的成绩作为样本进行统计(该校全体学生的成绩均在[60,140),按照[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)的分组作出频率分布直方图如图1所示,样本中分数在[70,90)内的所有数据的茎叶图如图2所示.

根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
(1)求n和频率分布直方图中的x,y的值;
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(3)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用ξ表示所抽取的3 名学生中为重本的人数,求随机变量ξ的分布列和数学期望.

根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
| 分数 | [50,85] | [85,110] | [110,150] |
| 可能被录取院校层次 | 专科 | 本科 | 重本 |
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(3)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用ξ表示所抽取的3 名学生中为重本的人数,求随机变量ξ的分布列和数学期望.
18.《九章算术》教会了人们用等差数列的知识来解决问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织( )尺布.
| A. | $\frac{1}{2}$ | B. | $\frac{24}{29}$ | C. | $\frac{16}{31}$ | D. | $\frac{16}{29}$ |
8.设m,n是两条不同的直线,α,β是两个不同的平面,下列说法正确的是( )
| A. | 若m∥α,α∩β=n,则 m∥n | B. | 若m∥α,m⊥n,则n⊥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若m?α,n?β,α⊥β,则m⊥n |
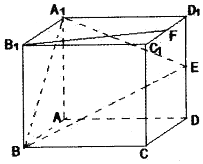 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.