题目内容
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,右焦点为F(c,0),弦PQ过F且垂直于x轴,过点P、点Q分别作直线AQ、AP的垂线,两垂线交于点B,若B到直线PQ的距离小于2(a+c),则该双曲线离心率的取值范围是( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
分析 求出直线BQ的方程,令y=0,可得B的坐标,利用B到直线PQ的距离小于2(a+c),得出a,c的关系,即可求出该双曲线离心率的取值范围.
解答 解:由题意,B在x轴上,P(c,$\frac{{b}^{2}}{a}$),Q(c,-$\frac{{b}^{2}}{a}$),∴kAQ=$\frac{\frac{{b}^{2}}{a}}{a-c}$,
∴kBP=-$\frac{{a}^{2}-ac}{{b}^{2}}$,
直线BQ的方程为y-$\frac{{b}^{2}}{a}$=-$\frac{{a}^{2}-ac}{{b}^{2}}$(x-c),
令y=0,可得x=$\frac{{b}^{4}}{{a}^{2}(a-c)}$+c,
∵B到直线PQ的距离小于2(a+c),
∴-$\frac{{b}^{4}}{{a}^{2}(a-c)}$<2(a+c),
∴b<$\sqrt{2}$a,
∴c<$\sqrt{3}a$,
∴e<$\sqrt{3}$,
∵e>1,
∴1$<e<\sqrt{3}$,
故选A.
点评 本题考查双曲线的方程与性质,考查直线方程的求解,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知点A是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a,b>0)右支上一点,F是右焦点,若△AOF(O是坐标原点)是等边三角形,则该双曲线离心率e为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
16.为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$(n=a+b+c+d)
独立性检验临界值表:
| 喜好体育运动 | 不喜好体育运动 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$(n=a+b+c+d)
独立性检验临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
17.某学校为了解该校高三年级学生数学科学习情况,对广一模考试数学成绩进行分析,从中抽取了n 名学生的成绩作为样本进行统计(该校全体学生的成绩均在[60,140),按照[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)的分组作出频率分布直方图如图1所示,样本中分数在[70,90)内的所有数据的茎叶图如图2所示.

根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
(1)求n和频率分布直方图中的x,y的值;
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(3)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用ξ表示所抽取的3 名学生中为重本的人数,求随机变量ξ的分布列和数学期望.

根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
| 分数 | [50,85] | [85,110] | [110,150] |
| 可能被录取院校层次 | 专科 | 本科 | 重本 |
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(3)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用ξ表示所抽取的3 名学生中为重本的人数,求随机变量ξ的分布列和数学期望.
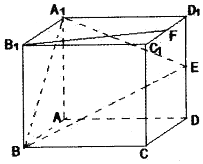 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.