题目内容
20.设函数f(x)=x3-3x+1,x∈[-2,2]的最大值为M,最小值为m,则M+m=2.分析 求出原函数的导函数,得到导函数的零点,进一步得到原函数的极值点,求得极值,再求出端点值,比较可得最大值为M,最小值为m,则M+m可求.
解答 解:由f(x)=x3-3x+1,得f′(x)=3x2-3=3(x+1)(x-1),
当x∈(-2,-1)∪(1,2)时,f′(x)>0,当x∈(-1,1)时,f′(x)<0.
∴函数f(x)的增区间为(-2,-1),(1,2);减区间为(-1,1).
∴当x=-1时,f(x)有极大值3,当x=1时,f(x)有极小值-1.
又f(-2)=-1,f(2)=3.
∴最大值为M=3,最小值为m=-1,
则M+m=3-1=2.
故答案为:2.
点评 本题考查利用导数求函数在闭区间上的最值,考查函数的导数的应用,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.设x,y满足约束条件$\left\{\begin{array}{l}x≥y\\ y≥4x-3\\ x≥0,y≥0\end{array}\right.$,若目标函数2z=2x+ny(n>0),z的最大值为2,则$y=tan({nx+\frac{π}{6}})$的图象向右平移$\frac{π}{6}$后的表达式为( )
| A. | $y=tan({2x+\frac{π}{6}})$ | B. | $y=cot({x-\frac{π}{6}})$ | C. | $y=tan({2x-\frac{π}{6}})$ | D. | y=tan2x |
8.某公司的班车分别在7:30,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过15分钟的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{8}$ |
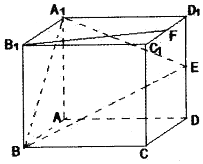 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.