题目内容
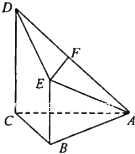 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.(Ⅰ)求证:EF∥平面ABC;
(Ⅱ)求证:平面ADE⊥平面ACD;
(Ⅲ)求直线AE和平面BCDE所成角的正弦值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)取AC中点G,连接FG、BG,根据三角形中位线定理,得到四边形FGBE为平行四边形,进而得到EF∥BG,再结合线面平行的判定定理得到EF∥面ABC;
(Ⅱ)根据已知中△ABC为等边三角形,G为AC的中点,DC⊥面ABC得到BG⊥AC,DC⊥BG,根据线面垂直的判定定理得到BG⊥面ADC,则EF⊥面ADC,再由面面垂直的判定定理,可得面ADE⊥面ACD;
(Ⅲ)建立坐标系,求出平面BCDE的法向量,利用向量的夹角公式,即可求直线AE和平面BCDE所成角的正弦值.
(Ⅱ)根据已知中△ABC为等边三角形,G为AC的中点,DC⊥面ABC得到BG⊥AC,DC⊥BG,根据线面垂直的判定定理得到BG⊥面ADC,则EF⊥面ADC,再由面面垂直的判定定理,可得面ADE⊥面ACD;
(Ⅲ)建立坐标系,求出平面BCDE的法向量,利用向量的夹角公式,即可求直线AE和平面BCDE所成角的正弦值.
解答:
 (Ⅰ)证明:取AC中点G,连接FG、BG,
(Ⅰ)证明:取AC中点G,连接FG、BG,
∵F,G分别是AD,AC的中点
∴FG∥CD,且FG=
DC=1.
∵BE∥CD∴FG与BE平行且相等
∴EF∥BG.
EF?面ABC,BG?面ABC
∴EF∥面ABC;
(Ⅱ)证明:∵△ABC为等边三角形∴BG⊥AC
又∵DC⊥面ABC,BG?面ABC,
∴DC⊥BG
∴BG垂直于面ADC的两条相交直线AC,DC,
∴BG⊥面ADC.
∵EF∥BG
∴EF⊥面ADC
∵EF?面ADE,∴面ADE⊥面ADC;
(Ⅲ)解:建立如图所示的坐标系,则A(0,
,0),E(1,0,1),B(1,0,0),C(0,-
,0)
∴
=(1,-
,1),
=(-1,-
,0),
=(0,0,1)
设平面BCDE的法向量为
=(x,y,z),则
,故取
=(1,-2,0)
∴直线AE和平面BCDE所成角的正弦值为|
|=
.
 (Ⅰ)证明:取AC中点G,连接FG、BG,
(Ⅰ)证明:取AC中点G,连接FG、BG,∵F,G分别是AD,AC的中点
∴FG∥CD,且FG=
| 1 |
| 2 |
∵BE∥CD∴FG与BE平行且相等
∴EF∥BG.
EF?面ABC,BG?面ABC
∴EF∥面ABC;
(Ⅱ)证明:∵△ABC为等边三角形∴BG⊥AC
又∵DC⊥面ABC,BG?面ABC,
∴DC⊥BG
∴BG垂直于面ADC的两条相交直线AC,DC,
∴BG⊥面ADC.
∵EF∥BG
∴EF⊥面ADC
∵EF?面ADE,∴面ADE⊥面ADC;
(Ⅲ)解:建立如图所示的坐标系,则A(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AE |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BE |
设平面BCDE的法向量为
| n |
|
| n |
∴直线AE和平面BCDE所成角的正弦值为|
| 1+1 | ||||||
|
4
| ||
| 15 |
点评:本题考查的知识点是直线与平面平行的判定,平面与平面垂直的判定,线面角,其中熟练掌握空间线面平行或垂直的判定、性质、定义、几何特征是解答此类问题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知双曲线
-
=1,(a>b>0),两渐近线的夹角为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2或
|
 如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证:
如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证: