题目内容
 如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证:
如图在四棱锥P-ABCD中,底面ABCD是菱形,O是AC,BD的交点,PA=PC,PB=PD,E是PC上一点.求证:(1)PO⊥AB;
(2)平面PAC⊥平面BDE.
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证明PO⊥AB,只要证明PO⊥底面ABCD,只要证明PO⊥AC,PO⊥BD,根据已知条件即可求证;
(2)要证明平面PAC⊥平面BDE,只要证明BD⊥平面PAC,根据菱形的性质可以得出.
(2)要证明平面PAC⊥平面BDE,只要证明BD⊥平面PAC,根据菱形的性质可以得出.
解答:
 证明:(1)∵PA=PC,PB=PD,
证明:(1)∵PA=PC,PB=PD,
∴PO⊥AC,PO⊥BD,
∵AC∩BD=O,
∴PO⊥底面ABCD,
∵AB?平面ABCD,
∴PO⊥AB;
(2)∵底面ABCD是菱形,
∴BD⊥AC,
又PO⊥BD,PO∩AC=O,
∴BD⊥平面PAC,
又∵BD?平面BDE,
∴平面PAC⊥平面BDE.
 证明:(1)∵PA=PC,PB=PD,
证明:(1)∵PA=PC,PB=PD,∴PO⊥AC,PO⊥BD,
∵AC∩BD=O,
∴PO⊥底面ABCD,
∵AB?平面ABCD,
∴PO⊥AB;
(2)∵底面ABCD是菱形,
∴BD⊥AC,
又PO⊥BD,PO∩AC=O,
∴BD⊥平面PAC,
又∵BD?平面BDE,
∴平面PAC⊥平面BDE.
点评:本题主要考查了线线垂直与线面垂直,面面的垂直的关系,关键是找出它们之间的转化关系,属于基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知
1,
2是一对不共线向量,若
=
1+λ
2,
=-2λ
1-
2且
,
共线,则λ的值为( )
| e |
| e |
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
A、±
| ||||
B、±
| ||||
C、
| ||||
D、-
|
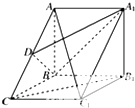 如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.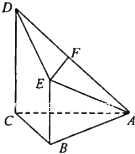 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.