题目内容
已知函数f（x）=2x3-3x2-12x+8．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若x∈[-2，3]，求函数f（x）的值域．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若x∈[-2，3]，求函数f（x）的值域．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：（Ⅰ）由函数f（x）=2x3-3x2-12x+8，得f′（x）=6x2-6x-12，令f′（x）=0时，解得：x=2，x=-1，从而求出函数的单调区间．
（Ⅱ）由（Ⅰ）得：f（x）在[-2，-1]，[2，3]递增，在（-1，2）递减，再求出极值和端点值，从而求出函数的值域．
（Ⅱ）由（Ⅰ）得：f（x）在[-2，-1]，[2，3]递增，在（-1，2）递减，再求出极值和端点值，从而求出函数的值域．
解答：
解：（Ⅰ）∵函数f（x）=2x3-3x2-12x+8，
∴f′（x）=6x2-6x-12，
令f′（x）=0时，解得：x=2，x=-1，
∴f（x）在（-∞-1），（2，+∞）递增，在（-1，2）递减；
（Ⅱ）由（Ⅰ）得：
f（x）在[-2，-1]，[2，3]递增，在（-1，2）递减，
而f（-2）=4，f（-1）=15，f（2）=-12，f（3）=-1，
∴函数f（x）的值域为：[-12，15]．
∴f′（x）=6x2-6x-12，
令f′（x）=0时，解得：x=2，x=-1，
∴f（x）在（-∞-1），（2，+∞）递增，在（-1，2）递减；
（Ⅱ）由（Ⅰ）得：
f（x）在[-2，-1]，[2，3]递增，在（-1，2）递减，
而f（-2）=4，f（-1）=15，f（2）=-12，f（3）=-1，
∴函数f（x）的值域为：[-12，15]．
点评：本题考察了函数的单调性，求函数在闭区间上的最值问题，是一道基础题．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
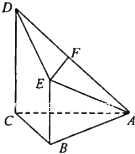已知四棱锥A-BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥平面ABC，BE∥CD，F为AD的中点．
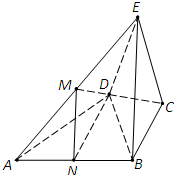如图，在四棱锥E-ABCD中，△ABD为正三角形，EB=ED，CB=CD．