题目内容
若中心在坐标原点,对称轴为坐标轴的椭圆经过点(4,0),离心率为
,求椭圆的标准方程.
| ||
| 2 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:利用椭圆的简单性质直接求解,需要注意的是要分焦点在x轴和焦点在y轴两种情况分别求解.
解答:
解:①焦点在x轴上时,
由题意知a=4,
=
,
解得c=2
,b2=a2-c2=16-12=4,
∴椭圆的标准方程为
+
=1.
②焦点在y轴上时,
由题意可知b=4,
=
,且a2=b2+c2,
解得c2=48,a2=64,
∴椭圆的标准方程为
+
=1.
由题意知a=4,
| c |
| a |
| ||
| 2 |
解得c=2
| 3 |
∴椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 4 |
②焦点在y轴上时,
由题意可知b=4,
| c |
| a |
| ||
| 2 |
解得c2=48,a2=64,
∴椭圆的标准方程为
| y2 |
| 64 |
| x2 |
| 16 |
点评:本题考查椭圆的标准方程的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
在△ABC中,若最大角的正弦值是
,则△ABC必是( )
| ||
| 2 |
| A、等边三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
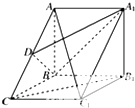 如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.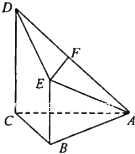 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.