题目内容
已知a,b都是实数,且a≠0,f(x)=|x-1|+|x-2|.
(1)求不等式f(x)>2的解集;
(2)若f(x)≤
对满足条件的所有实数a,b都成立,求实数x的取值范围.
(1)求不等式f(x)>2的解集;
(2)若f(x)≤
| |a+b|+|a-b| |
| |a| |
考点:绝对值不等式的解法,绝对值三角不等式
专题:不等式的解法及应用
分析:(1)化简函数f(x)的解析式,由f(x)>2得
,或
.求出每个不等式组的解集,再取并集,即得所求.
(2)求得
的最小值为2,可得f(x)≤2.再根据f(x)>2的解集,求得f(x)≤2的解集.
|
|
(2)求得
| |a+b|+|a-b| |
| |a| |
解答:
解:(1)由题意可得 f(x)=
,
由f(x)>2得
,或
.
解得x<
,或x>
,
即不等式的解集为(-∞,
)∪(
,+∞).
(2)∵
≥
=2,
∴f(x)≤2.
∵f(x)>2的解为x<
,或x>
,
∴f(x)≤2的解为
≤x≤
.
∴所求实数x的范围为[
,
].
|
由f(x)>2得
|
|
解得x<
| 1 |
| 2 |
| 5 |
| 2 |
即不等式的解集为(-∞,
| 1 |
| 2 |
| 5 |
| 2 |
(2)∵
| |a+b|+|a-b| |
| |a| |
| |a+b+a-b| |
| |a| |
∴f(x)≤2.
∵f(x)>2的解为x<
| 1 |
| 2 |
| 5 |
| 2 |
∴f(x)≤2的解为
| 1 |
| 2 |
| 5 |
| 2 |
∴所求实数x的范围为[
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查带由绝对值的函数,绝对值不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
设f(x)=x2-2x-4lnx,则f(x)的增区间为( )
| A、(0,+∞) |
| B、(2,+∞) |
| C、(-∞,-1) |
| D、(∞,-1)和(2,+∞) |
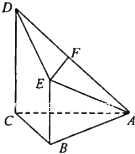 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.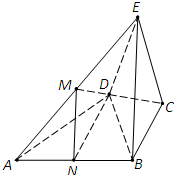 如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.
如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.