题目内容
设f(x)=ax3-
(a+2)x2+6x-3,x∈R,a是常数,且a>0
(1)求f(x)的单调递增区间;
(2)若f(x)在x=1时取得极大值,且直线y=-1与函数f(x)的图象有三个交点,求实数a的取值范围.
| 3 |
| 2 |
(1)求f(x)的单调递增区间;
(2)若f(x)在x=1时取得极大值,且直线y=-1与函数f(x)的图象有三个交点,求实数a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:分类讨论,导数的综合应用
分析:(1)对f(x)求导,讨论a取值,对应f′(x)的正负情况,得出f(x)的单调递增区间;
(2)由题意,结合(1)知0<a<2,求出f(x)的极大值与极小值,建立不等式组,求出a的取值范围.
(2)由题意,结合(1)知0<a<2,求出f(x)的极大值与极小值,建立不等式组,求出a的取值范围.
解答:
解:(1)∵f(x)=ax3-
(a+2)x2+6x-3,
∴f′(x)=3ax2-3(a+2)x+6=3(ax-2)(x-1);
①当0<a<2时,
>1,
由f′(x)=3(ax-2)(x-1)>0,得x<1或x>
,
∴f(x)的单调递增区间是(-∞,1)和(
,+∞);
②当a=2时,f′(x)=6(x-1)2≥0恒成立,
且只有f′(1)=0,
∴f(x)的单调递增区间是(-∞,+∞);
③当a>2时,有
<1,
由f′(x)=3(ax-2)(x-1)>0,得x<
或x>1,
∴f(x)的单调递增区间是(-∞,
)和(1,+∞);
(2)∵f(x)在x=1时取得极大值,
由(1)知,0<a<2,
∴f(x)|极大=f(1)=-
,
f(x)|极小=f(
)=-
+
-3,
∵直线y=-1与函数f(x)的图象有三个交点,
∴-
+
-3<-1<-
,
解得0<a<1;
∴a的取值范围是{a|0<a<2}.
| 3 |
| 2 |
∴f′(x)=3ax2-3(a+2)x+6=3(ax-2)(x-1);
①当0<a<2时,
| 2 |
| a |
由f′(x)=3(ax-2)(x-1)>0,得x<1或x>
| 2 |
| a |
∴f(x)的单调递增区间是(-∞,1)和(
| 2 |
| a |
②当a=2时,f′(x)=6(x-1)2≥0恒成立,
且只有f′(1)=0,
∴f(x)的单调递增区间是(-∞,+∞);
③当a>2时,有
| 2 |
| a |
由f′(x)=3(ax-2)(x-1)>0,得x<
| 2 |
| a |
∴f(x)的单调递增区间是(-∞,
| 2 |
| a |
(2)∵f(x)在x=1时取得极大值,
由(1)知,0<a<2,
∴f(x)|极大=f(1)=-
| a |
| 2 |
f(x)|极小=f(
| 2 |
| a |
| 4 |
| a2 |
| 6 |
| a |
∵直线y=-1与函数f(x)的图象有三个交点,
∴-
| 4 |
| a2 |
| 6 |
| a |
| a |
| 2 |
解得0<a<1;
∴a的取值范围是{a|0<a<2}.
点评:本题考查了导数的综合应用问题,解题时应利用导数的正负来研究函数的单调性,利用函数的单调性来研究函数的极值,是综合性题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图是5名学生一次数学测试成绩的茎叶图,则这5名学生该次测试成绩的方差为( )


| A、20 | B、21.2 |
| C、106 | D、127 |
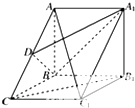 如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.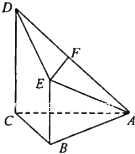 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.