题目内容
已知函数y=-sin2x-acosx+2,是否存在实数a,使得函数的最小值为-2,若存在,求出a的值;若不存在,请说明理由.
考点:三角函数的最值,二次函数在闭区间上的最值,余弦函数的定义域和值域
专题:三角函数的求值
分析:函数y=(cosx-
)2+1-
,再分当
≤-1、当-1<
<1时、当
≥1时三种情况,分别利用二次函数的性质求得y的最小值,再根据y的最小值为-2,求得a的值.
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:
解:∵y=cos2x-acosx+1=(cosx-
)2+1-
当
≤-1,即a≤-2时,则当cosx=-1时,ymin=2+a=-2,
∴a=-4.
当-1<
<1,即-2<a<2时,ymin=1-
=-2 得a2=12(舍).
当
≥1,即a≥2时,cosx=1时,ymin=2-a=-2,
∴a=4.
综上,存在a=-4或a=4时,函数的最小值为-2.
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
∴a=-4.
当-1<
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
∴a=4.
综上,存在a=-4或a=4时,函数的最小值为-2.
点评:本题主要考查余弦函数的定义域和值域,二次函数的性质应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
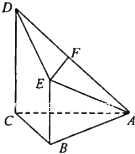 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥平面ABC,BE∥CD,F为AD的中点.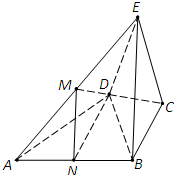 如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.
如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.