题目内容
已知双曲线
-
=1，（a＞b＞0），两渐近线的夹角为
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2或
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先由双曲线的两条渐近线的夹角为
，得双曲线的两条渐近线的斜率±
或±
，通过讨论分别计算离心率，由
=
或
，再由双曲线中c2=a2+b2，求其离心率即可．
| π |
| 3 |
| 3 |
| ||
| 3 |
| b |
| a |
| 3 |
| ||
| 3 |
解答：
解：∵双曲线的两条渐近线的夹角为60°，且渐近线关于x、y轴对称，
若夹角在x轴上，则双曲线的两条渐近线的倾斜角为30°，150°，斜率为±
；
若夹角在y轴上，则双曲线的两条渐近线的倾斜角为60°，120°，斜率为±
．
∴
=
或
，
∵c2=a2+b2
∴
=3或
=
，
∴e2-1=
或e2-1=3，
∴e=
或e=2．
故选D．
若夹角在x轴上，则双曲线的两条渐近线的倾斜角为30°，150°，斜率为±
| ||
| 3 |
若夹角在y轴上，则双曲线的两条渐近线的倾斜角为60°，120°，斜率为±
| 3 |
∴
| b |
| a |
| 3 |
| ||
| 3 |
∵c2=a2+b2
∴
| c2-a2 |
| a2 |
| c2-a2 |
| a2 |
| 1 |
| 3 |
∴e2-1=
| 1 |
| 3 |
∴e=
2
| ||
| 3 |
故选D．
点评：本题主要考查了双曲线的标准方程、双曲线的简单性质等基础知识，考查运算求解能力，考查分类讨论思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知a，b为不相等的两正数，且a3-b3=a2-b2，则a+b的取值范围是（ ）
A、（0，
| ||
B、（1，
| ||
C、（
| ||
| D、（1，2） |
已知
1，
2是一对不共线向量，若
=
1+λ
2，
=-2λ
1-
2且
，
共线，则λ的值为（ ）
| e |
| e |
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
A、±
| ||||
B、±
| ||||
C、
| ||||
D、-
|
如图是5名学生一次数学测试成绩的茎叶图，则这5名学生该次测试成绩的方差为（ ）
| A、20 | B、21.2 |
| C、106 | D、127 |
设f（x）=x2-2x-4lnx，则f（x）的增区间为（ ）
| A、（0，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（∞，-1）和（2，+∞） |
在△ABC中，若最大角的正弦值是
，则△ABC必是（ ）
| ||
| 2 |
| A、等边三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
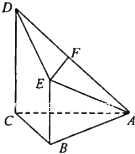已知四棱锥A-BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥平面ABC，BE∥CD，F为AD的中点．