题目内容
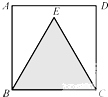如图，正方形ABCD的边长为2，△EBC为正三角形．若向正方形ABCD内随机投掷一个质点，则它落在△EBC内的概率为考点：几何概型
专题：概率与统计
分析：根据已知，计算出正方形ABCD和△EBC的面积，代入几何概型概率计算公式，可得答案．
解答：
解：∵正方形ABCD的边长为2，
∴正方形ABCD的面积为4，
又∵△EBC为正三角形．
∴△EBC的面积为：
×22=
，
故向正方形ABCD内随机投掷一个质点，则它落在△EBC内的概率P=
，
故答案为：
∴正方形ABCD的面积为4，
又∵△EBC为正三角形．
∴△EBC的面积为：
| ||
| 4 |
| 3 |
故向正方形ABCD内随机投掷一个质点，则它落在△EBC内的概率P=
| ||
| 4 |
故答案为：
| ||
| 4 |
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=N（A）/N求解．
练习册系列答案
53随堂测系列答案
相关题目
在正方体ABCD-A1B1C1D1 中，其棱长为1，则列命题中正确命题的个数为（ ）
（1）A1C1和AD1所成角为
（2）B1到截面A1C1D的距离为
（3）正方体的内切球与外接球的半径比为1：
．
（1）A1C1和AD1所成角为
| π |
| 3 |
（2）B1到截面A1C1D的距离为
2
| ||
| 3 |
（3）正方体的内切球与外接球的半径比为1：
| 2 |
| A、0 | B、1 | C、2 | D、3 |
二次函数y=x2+ax+b中，若a+b=0，则它的图象必经过点（ ）
| A、（-1，-1） |
| B、（1，-1） |
| C、（1，1） |
| D、（-1，1） |
tan1815°+cot
=（ ）
| 13π |
| 12 |
| A、2 | ||||
| B、2 | ||||
| C、4 | ||||
D、
|
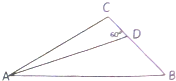爸爸去哪儿节目组安排星娃们露营，村长要求，Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷，AB=8米，BC=4米，AC=6米．现村长给多多一个难题，要求她安扎在B、C两点连线段上的D点位置，∠ADC=60°，如图所示，问多多与Feyman相距多少米？