题目内容
在正方体ABCD-A1B1C1D1 中,其棱长为1,则列命题中正确命题的个数为( )
(1)A1C1和AD1所成角为
(2)B1到截面A1C1D的距离为
(3)正方体的内切球与外接球的半径比为1:
.
(1)A1C1和AD1所成角为
| π |
| 3 |
(2)B1到截面A1C1D的距离为
2
| ||
| 3 |
(3)正方体的内切球与外接球的半径比为1:
| 2 |
| A、0 | B、1 | C、2 | D、3 |
考点:球内接多面体,棱柱的结构特征
专题:空间位置关系与距离
分析:(1)首先,连结AC、CD1、AD1,则∠CAD1就是A1C1和AD1所成角,然后求解即可;
(2)可以利用等积法求解其高;
(3)正方体的内切球半径就是棱长的一半,外接球的直径就是正方体的体对角线.
(2)可以利用等积法求解其高;
(3)正方体的内切球半径就是棱长的一半,外接球的直径就是正方体的体对角线.
解答:
解:对于(1)如图
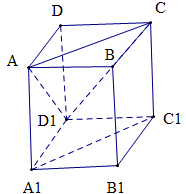
连结AC、CD1、AD1,
则∠CAD1就是A1C1和AD1所成角,
在等边△ACD1中,
∴∠CAD1=
,故(1)正确;
对于(2)如图:
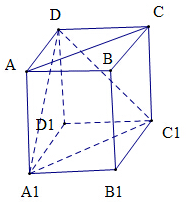
V三棱锥B1-A1C1D=V三棱锥D-A1B1C1,
即
S△A1C1D×h=
S△A1B1C1×a,
∴h=
.
故(2)错误;
对于(3):
设正方体的棱长为2a,
则正方体的内切球半径就是棱长的一半,
即r=a,
外接球的直径就是正方体的体对角线,即
R=
a,
∴r:R=1:
,
故(3)错误,
综上,只有(1)正确;
故选:B.

连结AC、CD1、AD1,
则∠CAD1就是A1C1和AD1所成角,
在等边△ACD1中,
∴∠CAD1=
| π |
| 3 |
对于(2)如图:

V三棱锥B1-A1C1D=V三棱锥D-A1B1C1,
即
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
| ||
| 3 |
故(2)错误;
对于(3):
设正方体的棱长为2a,
则正方体的内切球半径就是棱长的一半,
即r=a,
外接球的直径就是正方体的体对角线,即
R=
| 3 |
∴r:R=1:
| 3 |

故(3)错误,
综上,只有(1)正确;
故选:B.
点评:本题重点考查了正方体中的边角关系、线线平行、体积公式等知识,属于中档题.解题关键是正确添加辅助线和等积法在求解距离中的灵活运用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知函数f(x)=x3-
x2sinθ,其中x∈R,θ为参数,且0≤θ≤π.若函数f(x)的极小值小于-
,则参数θ的取值范围是( )
| 3 |
| 4 |
| 1 |
| 128 |
A、(
| ||||
B、(
| ||||
C、[
| ||||
D、(
|
已知A、B、C三点在球心为O,半径为3的球面上,且三棱锥O-ABC为正四面体,那么A、B两点间的球面距离为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
函数f(x)=lnx-
的零点所在的区间是( )
| 3 |
| x |
| A、(1,2) |
| B、(1,e) |
| C、(e,3) |
| D、(e,+∞) |

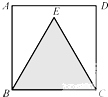 如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为
如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为