题目内容
已知函数f（x）=cos4x-2sinxcosx-sin4x．
（1）求f（x）的最小正周期；
（2）若x∈（
，
），求f（x）的最大值及最小值；
（3）若函数g（x）=f（-x），求g（x）的单调增区间．
（1）求f（x）的最小正周期；
（2）若x∈（
| π |
| 4 |
| 5π |
| 12 |
（3）若函数g（x）=f（-x），求g（x）的单调增区间．
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）化简可得f（x）=
cos（2x+
），从而可求f（x）的最小正周期；
（2）若x∈（
，
），可求得2x-
∈（
，
），即可求得当x=
时，f（x）的最大值为-1；当x=
时，f（x）的最小值为-
．
（3）g（x）=f（-x）=
cos（-2x+
）=
cos（2x-
）．由2kπ≤2x-
≤2kπ+π，解得kπ+
≤x≤kπ+
，由2kπ-π≤2x-
≤2kπ，可解得kπ-
≤x≤kπ+
，从而得到g（x）的单调增区间．
| 2 |
| π |
| 4 |
（2）若x∈（
| π |
| 4 |
| 5π |
| 12 |
| π |
| 4 |
| 3π |
| 4 |
| 13π |
| 12 |
| π |
| 4 |
| 3π |
| 8 |
| 2 |
（3）g（x）=f（-x）=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 5π |
| 8 |
| π |
| 4 |
| 3π |
| 8 |
| π |
| 8 |
解答：
解：（1）由题知f（x）=（cos2x-sin2x）（cos2x+sin2x）-sin2x=cos2x-sin2x=
cos（2x+
）
所以f（x）的最小正周期T=
=π．
（2）因为x∈（
，
），所以2x-
∈（
，
），
所以f（x）∈[-
，-1]．
所以当x=
时，f（x）的最大值为-1；当x=
时，f（x）的最小值为-
．
（3）g（x）=f（-x）=
cos（-2x+
）=
cos（2x-
）．
由2kπ≤2x-
≤2kπ+π，解得kπ+
≤x≤kπ+
，
函数f（x）的单调减区间为[kπ+
，kπ+
]（k∈Z）．
由2kπ-π≤2x-
≤2kπ，解得kπ-
≤x≤kπ+
，
函数f（x）的单调增区间为[kπ-
，kπ+
]（k∈Z）．
注意：其它的解题方案导致其它的解题结果．
| 2 |
| π |
| 4 |
所以f（x）的最小正周期T=
| 2π |
| 2 |
（2）因为x∈（
| π |
| 4 |
| 5π |
| 12 |
| π |
| 4 |
| 3π |
| 4 |
| 13π |
| 12 |
所以f（x）∈[-
| 2 |
所以当x=
| π |
| 4 |
| 3π |
| 8 |
| 2 |
（3）g（x）=f（-x）=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
由2kπ≤2x-
| π |
| 4 |
| π |
| 8 |
| 5π |
| 8 |
函数f（x）的单调减区间为[kπ+
| π |
| 8 |
| 5π |
| 8 |
由2kπ-π≤2x-
| π |
| 4 |
| 3π |
| 8 |
| π |
| 8 |
函数f（x）的单调增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
注意：其它的解题方案导致其它的解题结果．
点评：本题主要考察了三角函数中的恒等变换应用，正弦函数的图象和性质，属于中档题．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
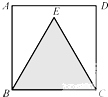如图，正方形ABCD的边长为2，△EBC为正三角形．若向正方形ABCD内随机投掷一个质点，则它落在△EBC内的概率为