题目内容
若数列{An}满足An+1=An2,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=9,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n为正整数.
(Ⅰ)证明数列{an+1}是“平方递推数列”,且数列{lg(an+1)}为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前n项积为Tn,即Tn=(a1+1)(a2+1)…(an+1),求lgTn;
(Ⅲ)在(Ⅱ)的条件下,记bn=
,求数列{bn}的前n项和为Sn,并求使Sn>2014的n的最小值.
(Ⅰ)证明数列{an+1}是“平方递推数列”,且数列{lg(an+1)}为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前n项积为Tn,即Tn=(a1+1)(a2+1)…(an+1),求lgTn;
(Ⅲ)在(Ⅱ)的条件下,记bn=
| lgTn |
| lg(an+1) |
考点:数列与函数的综合
专题:计算题,证明题,新定义,等差数列与等比数列
分析:(I)代入点,得到递推式,配方,由新定义,即可判断,再两边取对数,由等比数列的定义,即可得证;
(II)由对数的运算性质和等比数列的求和公式,即可得到;
(III)运用分组求和方法,结合等差数列和等比数列的求和公式,通过判断n的范围解不等式,即可得到最小值.
(II)由对数的运算性质和等比数列的求和公式,即可得到;
(III)运用分组求和方法,结合等差数列和等比数列的求和公式,通过判断n的范围解不等式,即可得到最小值.
解答:
(I)证明:由题意得:an+1=
+2an,
即 an+1+1=(an+1)2,
则{an+1}是“平方递推数列”.
又有lg(an+1+1)=2lg(an+1)得
{lg(an+1)}是以lg(a1+1)为首项,2为公比的等比数列;
(II)解:由(I)知lg(an+1)=lg(a1+1)•2n-1=2n-1,lgTn=lg(a1+1)(a2+1)…(an+1)=lg(a1+1)+lg(a2+1)+…+lg(an+1)=
=2n-1.
(III)解:bn=
=
=2-(
)n-1,
Sn=2n-
=2n-2+
,
又Sn>2014,即2n-2+
>2014,
n+
>1008,
又 0<
<1,
则nmin=1008.
| a | 2 n |
即 an+1+1=(an+1)2,
则{an+1}是“平方递推数列”.
又有lg(an+1+1)=2lg(an+1)得
{lg(an+1)}是以lg(a1+1)为首项,2为公比的等比数列;
(II)解:由(I)知lg(an+1)=lg(a1+1)•2n-1=2n-1,lgTn=lg(a1+1)(a2+1)…(an+1)=lg(a1+1)+lg(a2+1)+…+lg(an+1)=
| 1(1-2n) |
| 1-2 |
(III)解:bn=
| lgTn |
| lg(an+1) |
| 2n-1 |
| 2n-1 |
| 1 |
| 2 |
Sn=2n-
1-
| ||
1-
|
| 1 |
| 2n-1 |
又Sn>2014,即2n-2+
| 1 |
| 2n-1 |
n+
| 1 |
| 2n |
又 0<
| 1 |
| 2n |
则nmin=1008.
点评:本题考查新定义的理解和运用,考查等比数列的通项公式和求和公式的运用,考查数列的求和方法:分组求和,考查判断和运算能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知函数f(x)=x3-
x2sinθ,其中x∈R,θ为参数,且0≤θ≤π.若函数f(x)的极小值小于-
,则参数θ的取值范围是( )
| 3 |
| 4 |
| 1 |
| 128 |
A、(
| ||||
B、(
| ||||
C、[
| ||||
D、(
|
若O为△ABC的内心,且满足(
-
)•(
+
-2
)=0,则△ABC的形状为( )
| OB |
| OC |
| OB |
| OC |
| OA |
| A、等腰三角形 | B、正三角形 |
| C、直角三角形 | D、以上都不对 |
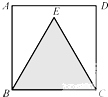 如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为
如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为