题目内容
解不等式x2+mx+n>0的解集为{x|x>5或x<-1},求实数m,n的值.
考点:一元二次不等式的解法
专题:计算题,函数的性质及应用
分析:由不等式x2+mx+n>0的解集为{x|x>5或x<-1}可得-1,5是方程x2+mx+n=0的两个根,从而利用韦达定理求解.
解答:
解:∵不等式x2+mx+n>0的解集为{x|x>5或x<-1},
∴-1,5是方程x2+mx+n=0的两个根,
∴-1+5=-m,-1×5=n,
解得,m=-4,n=-5.
∴-1,5是方程x2+mx+n=0的两个根,
∴-1+5=-m,-1×5=n,
解得,m=-4,n=-5.
点评:本题考查了方程与不等式的关系,属于基础题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知函数f(x)=x3-
x2sinθ,其中x∈R,θ为参数,且0≤θ≤π.若函数f(x)的极小值小于-
,则参数θ的取值范围是( )
| 3 |
| 4 |
| 1 |
| 128 |
A、(
| ||||
B、(
| ||||
C、[
| ||||
D、(
|
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )
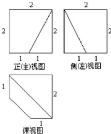

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
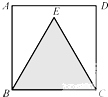 如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为
如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为