题目内容
所有棱长都为2的正三棱锥的体积为 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:由已知中正四面体的所有棱长都为2,我们可分别求出棱锥的底面面积和高,代入棱锥体积公式,即可得到答案.
解答:
解:当棱长为2时
正四面体的底面积S=
×22=
正四面体的高h=
×2=
故正四面体的体积V=
•S•h=
.
故答案为:
.
正四面体的底面积S=
| ||
| 4 |
| 3 |
正四面体的高h=
| ||
| 3 |
2
| ||
| 3 |
故正四面体的体积V=
| 1 |
| 3 |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查的知识点是棱锥的体积公式,由于正四面体在考试中比较容易考查,故熟练掌握棱长为a的正四面体的底面积、高、体积、表面积、内切球半径、外切球半径…的公式,是提高解答正四面体问题速度和精度的关键.

练习册系列答案
相关题目
已知函数f(x)=x3-
x2sinθ,其中x∈R,θ为参数,且0≤θ≤π.若函数f(x)的极小值小于-
,则参数θ的取值范围是( )
| 3 |
| 4 |
| 1 |
| 128 |
A、(
| ||||
B、(
| ||||
C、[
| ||||
D、(
|
若O为△ABC的内心,且满足(
-
)•(
+
-2
)=0,则△ABC的形状为( )
| OB |
| OC |
| OB |
| OC |
| OA |
| A、等腰三角形 | B、正三角形 |
| C、直角三角形 | D、以上都不对 |
已知A、B、C三点在球心为O,半径为3的球面上,且三棱锥O-ABC为正四面体,那么A、B两点间的球面距离为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )
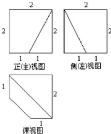

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
对于函数f(x)=
,下列命题正确的是( )
|
| A、值域[-1,1] | ||
B、当且仅当x=2kπ+
| ||
| C、最小正周期为π | ||
D、当且仅当2kπ+π<x<2kπ+
|
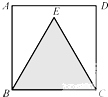 如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为
如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为