题目内容
tan1815°+cot
=( )
| 13π |
| 12 |
| A、2 | ||||
| B、2 | ||||
| C、4 | ||||
D、
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系、诱导公式,化简求得所给式子的值.
解答:
解:tan1815°+cot
=tan15°+cot
=tan15°+cot15°=
+
=
=
=4,
故选:C.
| 13π |
| 12 |
| π |
| 12 |
| sin15° |
| cos15° |
| cos15° |
| sin15° |
=
| sin215°+cos215° |
| sin15°cos15° |
| 1 | ||
|
故选:C.
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
若O为△ABC的内心,且满足(
-
)•(
+
-2
)=0,则△ABC的形状为( )
| OB |
| OC |
| OB |
| OC |
| OA |
| A、等腰三角形 | B、正三角形 |
| C、直角三角形 | D、以上都不对 |
已知A、B、C三点在球心为O,半径为3的球面上,且三棱锥O-ABC为正四面体,那么A、B两点间的球面距离为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
某几何体的三视图如图所示,则此几何体的体积等于( )


| A、30 | B、12 | C、24 | D、4 |
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )
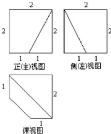

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
曲线y=x2-x+1在点(1,0)处的切线方程为( )
| A、y=x-1 |
| B、y=-x+1 |
| C、y=2x-2 |
| D、y=-2x+2 |
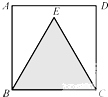 如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为
如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为