题目内容
已知向量
=(sinx,
sinx),
=(sinx,-cosx),设函数f(x)=
•
.
(1)求函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若f(A)+sin(2A-
)=1,b+c=7,△ABC的面积为2
,求边a的长.
| m |
| 3 |
| n |
| m |
| n |
(1)求函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若f(A)+sin(2A-
| π |
| 6 |
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(1)利用二倍角公式和两角和公式对函数解析式化简整理,进而根据正弦函数的性质确定函数的单调增区间.
(2)根据(1)中函数的解析式,根据f(A)+sin(2A-
)=1,求得A,根据三角形面积公式求得bc的值,利用余弦定理求得a.
(2)根据(1)中函数的解析式,根据f(A)+sin(2A-
| π |
| 6 |
解答:
解:(1)由题意得f(x)=sin2x-
sinxcosx=
-
sin2x=
-sin(2x+
),
令2kπ+
≤2x+
≤2kπ+
,k∈Z,
解得:kπ+
≤x≤kπ+
,k∈Z
所以函数f(x)的单调递增区间为[kπ+
,kπ+
],k∈Z
(2)由f(A)+sin(2A-
)=1得:
-sin(2A+
)+sin(2A-
)=1,
化简得:cos2A=-
,
又因为0<A<
,解得:A=
,
由题意知:S△ABC=
bcsinA=2
,解得bc=8,
又b+c=7,所以a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=49-2×8×(1+
)=25,
∴a=5
| 3 |
| 1-cos2x |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解得:kπ+
| π |
| 6 |
| 2π |
| 3 |
所以函数f(x)的单调递增区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
(2)由f(A)+sin(2A-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
化简得:cos2A=-
| 1 |
| 2 |
又因为0<A<
| π |
| 2 |
| π |
| 3 |
由题意知:S△ABC=
| 1 |
| 2 |
| 3 |
又b+c=7,所以a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=49-2×8×(1+
| 1 |
| 2 |
∴a=5
点评:本题只要考查了三角函数恒等变换的应用,三角函数图象与性质,余弦定理的应用.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
在△ABC中,若sin2B=sin2C,则△ABC为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等边三角形 |
| D、等腰或直角三角形 |
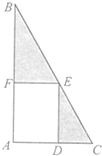 某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=
某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=