题目内容
已知圆O的方程为x2+y2=13,直线l:x0x+y0y=13,设点A(x0,y0).
(1)若点A为(3,4),试判断直线l与圆C的位置关系;
(2)若点A在圆O上,且x0=2,y0>0,过点A作直线AM,AN分别交圆O于M,N两点,且直线AM和AN的斜率互为相反数.
①若直线AM过点O,求直线MN的斜率;
②试问:不论直线AM的斜率怎样变化,直线MN的斜率是否为定值?若是,求出该定值;若不是,说明理由.
(1)若点A为(3,4),试判断直线l与圆C的位置关系;
(2)若点A在圆O上,且x0=2,y0>0,过点A作直线AM,AN分别交圆O于M,N两点,且直线AM和AN的斜率互为相反数.
①若直线AM过点O,求直线MN的斜率;
②试问:不论直线AM的斜率怎样变化,直线MN的斜率是否为定值?若是,求出该定值;若不是,说明理由.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)由点A在圆O外,求得圆心到直线的距离d小于半径,可得直线和圆相交.
(2)由条件求得点A(2,3).①若直线AM过点O,求得AM的斜率,可得AN的斜率kAN=-
,再利用两条直线的夹角公式求得直线MN的斜率.
②由直线AM和AN的倾斜角互补,可得△AMN为等腰三角形,直线MN平行于x轴,故MN的斜率是0,为定值.
(2)由条件求得点A(2,3).①若直线AM过点O,求得AM的斜率,可得AN的斜率kAN=-
| 3 |
| 2 |
②由直线AM和AN的倾斜角互补,可得△AMN为等腰三角形,直线MN平行于x轴,故MN的斜率是0,为定值.
解答:
解:(1)当点A的坐标为(3,4)时,直线l的方程为3x+4y-13=0,
圆心到直线l的距离d=
=
<
=r,
∴直线l与圆O相交.…(5分)
(2)①由点A在圆O上,且x0=2,y0>0,得y0=3,即A(2,3).
由题意,AM是圆的直径,所以点M的坐标为(-2,-3),且kAM=
.
又直线AM和AN的斜率互为相反数,所以kAN=-
…(7分)
直线AN的方程为y=-
x+6,由
得:x2+(6-
x)2=13,
解得:x=2或x=
,所以N(
,
)
∴直线MN的斜率为kMN=
=
=
.…(10分)
②记直线AM的斜率为k,则直线AM的方程为:y=kx+3-2k.
将y=kx+3-2k代入圆O的方程得:x2+(kx+3-2k)2=13,
化简得:(k2+1)x2+2k(3-2k)x+(3-2k)2-13=0,
∵2是方程的一个根,∴2xM=
,∴xM=
,
由题意知:kAN=-k,同理可得,xN=
,…(13分)
∴kMN=
=
=k
,
∴kMN=k•
=k•
=
,
∴不论直线AM的斜率怎样变化,直线MN的斜率总为定值
.…(16分)
圆心到直线l的距离d=
| 13 | ||
|
| 13 |
| 5 |
| 13 |
∴直线l与圆O相交.…(5分)
(2)①由点A在圆O上,且x0=2,y0>0,得y0=3,即A(2,3).
由题意,AM是圆的直径,所以点M的坐标为(-2,-3),且kAM=
| 3 |
| 2 |
又直线AM和AN的斜率互为相反数,所以kAN=-
| 3 |
| 2 |
直线AN的方程为y=-
| 3 |
| 2 |
|
| 3 |
| 2 |
解得:x=2或x=
| 46 |
| 13 |
| 46 |
| 13 |
| 9 |
| 13 |
∴直线MN的斜率为kMN=
| ||
|
| ||
|
| 2 |
| 3 |
②记直线AM的斜率为k,则直线AM的方程为:y=kx+3-2k.
将y=kx+3-2k代入圆O的方程得:x2+(kx+3-2k)2=13,
化简得:(k2+1)x2+2k(3-2k)x+(3-2k)2-13=0,
∵2是方程的一个根,∴2xM=
| (3-2k)2-13 |
| k2+1 |
| 2k2-6k-2 |
| k2+1 |
由题意知:kAN=-k,同理可得,xN=
| 2k2+6k-2 |
| k2+1 |
∴kMN=
| yM-yN |
| xM-xN |
| kxM+3-2k-(-kxN+3+2k) |
| xM-xN |
| xM+xN-4 |
| xM-xN |
∴kMN=k•
| ||||
|
| ||
|
| 2 |
| 3 |
∴不论直线AM的斜率怎样变化,直线MN的斜率总为定值
| 2 |
| 3 |
点评:本题主要考查点和圆的位置关系,直线和圆的位置关系,直线的倾斜角和斜率,两条直线的夹角公式的应用,属于Z中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
正方体ABCD-A1B1C1D1的面BCC1B1内有一点M,满足∠MD1D=∠BD1D,则点M的轨迹是( )
| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
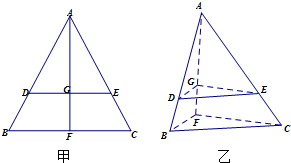 在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.
在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.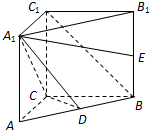 (理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=
(理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=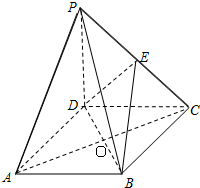 如图,在四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是边长为a的正方形,对角线AC与BD相交于O,且PD=a,E为棱PC的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是边长为a的正方形,对角线AC与BD相交于O,且PD=a,E为棱PC的中点.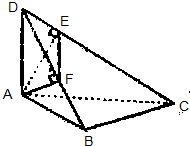 如图,在四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB,求证:
如图,在四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB,求证: