题目内容
在锐角△ABC中，已知
a=2csinA．
（1）确定角C的大小；
（2）若c=
，且S△ABC=
，求a+b的值．
| 3 |
（1）确定角C的大小；
（2）若c=
| 7 |
3
| ||
| 2 |
考点：正弦定理
专题：解三角形
分析：（1）利用正弦定理把已知等式中的边转换成角的正弦，化简可求得sinC的值，进而求得C．
（2）先根据三角形面积公式求得ab的值，进而利用余弦定理和C求得a2+b2的值，最后通过配方法求得a+b．
（2）先根据三角形面积公式求得ab的值，进而利用余弦定理和C求得a2+b2的值，最后通过配方法求得a+b．
解答：
解：（1）∵
a=2csinA，
∴
sinA=2sinCsinA，
∵sinA≠0，
∴sinC=
，
∵0＜A＜
，
∴C=
．
（2）S△ABC=
absinC=
，
∴ab=6，
cosC=
=
=
，
∴a2+b2=13，
∴a+b=
=
=5．
| 3 |
∴
| 3 |
∵sinA≠0，
∴sinC=
| ||
| 2 |
∵0＜A＜
| π |
| 2 |
∴C=
| π |
| 3 |
（2）S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
∴ab=6，
cosC=
| a2+b2-c2 |
| 2ab |
| a2+b2-7 |
| 12 |
| 1 |
| 2 |
∴a2+b2=13，
∴a+b=
| a2+b2+2ab |
| 13+12 |
点评：本题主要考查了正弦定理和余弦定理的应用．在解三角形过程中往往需要用正弦定理和余弦定理对三角形问题进行边角问题的转化．
练习册系列答案
相关题目
角α的终边过点P（-4，3），则sin2α=（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
将6个相同的小球放入3个不同的盒子，要求每个盒子中至少有1个小球，且每个盒子中的小球个数都不同，则不同的放法共有（ ）
| A、4种 | B、6种 | C、8种 | D、10种 |
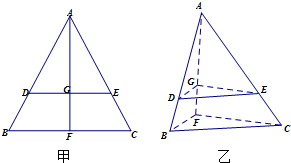在等边三角形ABC中，D、E分别是AB、BC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF折起，得到如图乙所示的三棱锥A-BCF．
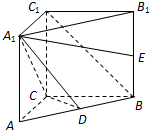（理科）如图，在直三棱柱ABC-A1B1C1中，∠ACB=