题目内容
已知
sinθ+cosθ=m+1,则实数m的取值范围是 .
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:先整理出已知等式表示出m,进而根据两角和公式对表达式化简,根据三角函数的性质求得m的范围.
解答:
解:依题意知m=
sinθ+cosθ-1=2sin(θ+
)-1,
∵-1≤sin(θ+
)≤1,
∴-3≤2sin(θ+
)-1≤1,
即m的范围为[-3,1].
故答案为:[-3,1].
| 3 |
| π |
| 6 |
∵-1≤sin(θ+
| π |
| 6 |
∴-3≤2sin(θ+
| π |
| 6 |
即m的范围为[-3,1].
故答案为:[-3,1].
点评:本题主要考查了两角和与差的正弦函数的应用.注意与三角函数的图象与性质相结合来解决问题.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn,且a1=1,a2=3,若对任意n∈N*,都有an+2-an=2成立,则S100=( )
| A、2550 | B、2600 |
| C、5050 | D、5100 |
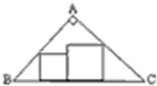 从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为
从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为