题目内容
某数学老师身高175cm，他爷爷、父亲和儿子的身高分别是172cm、169cm和181cm．已知儿子的身高与父亲的身高有关．
（1）列表（用表格表示题目中父子之间儿子的身高y与父亲的身高x对应关系）；
（2）用线性回归分析的方法预测该教师孙子的身高．
（1）列表（用表格表示题目中父子之间儿子的身高y与父亲的身高x对应关系）；
| 父亲的身高x（cm） | |||
| 儿子的身高y（cm） |
考点：线性回归方程
专题：计算题,概率与统计
分析：（1）根据题意可得三组父子的数据，填写表格；
（2）利用最小二乘法求回归系数，得回归直线方程，代入儿子的身高可得预报变量孙子的身高．
（2）利用最小二乘法求回归系数，得回归直线方程，代入儿子的身高可得预报变量孙子的身高．
解答：
解：（1）根据题意可得表格：
（2）
=
=173，
=
=175，
直接计算得
=
=
=1，
=
-
=175-1×172=3，
预测该教师孙子的身高y=
x+
=1×181+3=184cm．
| 父亲的身高x（cm） | 172 | 169 | 175 |
| 儿子的身高y（cm） | 169 | 175 | 181 |
. |
| x |
| 172+169+175 |
| 3 |
. |
| y |
| 169+175+181 |
| 3 |
直接计算得
| ? |
| b |
| |||||||
|
| 18 |
| 18 |
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
预测该教师孙子的身高y=
| ? |
| b |
| ? |
| a |
点评：本题考查了线性回归方程的求法及应用，熟练掌握最小二乘法求回归方程的系数是解题的关键．
练习册系列答案
相关题目
将6个相同的小球放入3个不同的盒子，要求每个盒子中至少有1个小球，且每个盒子中的小球个数都不同，则不同的放法共有（ ）
| A、4种 | B、6种 | C、8种 | D、10种 |
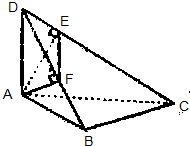如图，在四边形ABCD中，DA⊥平面ABC，∠ABC=90°，AE⊥CD，AF⊥DB，求证：