题目内容
已知△ABC中，
=
，
=
，当
、
满足下列条件式，能确定△ABC的形状吗？
（1）
•
＜0；
（2）
•
=0；
（3）
•
＞0．
| AB |
| a |
| AC |
| b |
| a |
| b |
（1）
| a |
| b |
（2）
| a |
| b |
（3）
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量数量积的定义，可得向量夹角的余弦值符号，从而判断∠BAC的大小．
解答：
解：因为
•
=|
||
|cos∠BAC，
所以（1）
•
＜0时，cos∠BAC＜0，所以∠BAC＞90°，△ABC是钝角三角形；
（2）
•
=0时，cos∠BAC=0，所以∠BAC=90°，△ABC是直角三角形；
（3）
•
＞0时，cos∠BAC＞0，所以∠BAC＜90°，但是不能判断三角形的形状．
| a |
| b |
| a |
| b |
所以（1）
| a |
| b |
（2）
| a |
| b |
（3）
| a |
| b |
点评：本题考查了运用向量数量积判断三角形内角的范围，属于基础题．
练习册系列答案
相关题目
如图所示，已知抛物线y=x2的动弦AB所在直线与圆x2+y2=1相切，分别过点A、B的抛物线的两条切线相交于点M，求点M的轨迹方程．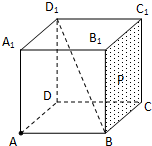
如图，棱长为1的正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总保持向量