题目内容
一条线段的长等于10,两端点A、B分别在x轴和y轴上滑动,M在线段AB上且
=4
,则点M的轨迹方程是 .
| AM |
| MB |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设M(x,y),A(a,0),B(0,b),根据
=4
,确定坐标之间的关系,代入a2+b2=100,可得结论.
| AM |
| MB |
解答:
解:设M(x,y),A(a,0),B(0,b)
则a2+b2=100,…①
∵
=4
,∴x=
a,y=
b,
由此可得a=5x且b=
y,代入①式可得25x2+
y2=100,
化简得16x2+y2=64,即为所求点M的轨迹方程.
故答案为:16x2+y2=64.
则a2+b2=100,…①
∵
| AM |
| MB |
| 1 |
| 5 |
| 4 |
| 5 |
由此可得a=5x且b=
| 5 |
| 4 |
| 25 |
| 16 |
化简得16x2+y2=64,即为所求点M的轨迹方程.
故答案为:16x2+y2=64.
点评:本题给出动点满足的条件,求动点的轨迹方程,考查向量的坐标运算、椭圆的定义与标准方程和动点轨迹的求法等知识,属于中档题.

练习册系列答案
相关题目
如图是一几何体的三视图,则该几何体的表面积是( )


A、5+
| ||
B、5+2
| ||
C、4+2
| ||
D、4+2
|
椭圆
(φ为参数)的长轴长为( )
|
| A、3 | B、5 | C、6 | D、10 |
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点(-2,3),则直线l的方程为( )
| A、x+y-3=0 |
| B、x+y-1=0 |
| C、x-y+5=0 |
| D、x-y-5=0 |
函数f(x)=sinx+
在区间[0,+∞)内( )
| x |
| A、没有零点 |
| B、有且仅有1个零点 |
| C、有且仅有2个零点 |
| D、有且仅有3个零点 |
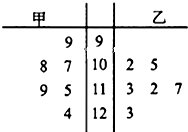 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示: