题目内容
为了对某课题进行研究，用分层抽样方法从三所高校A，B，C的相关人员中，抽取若干人组成研究小组、有关数据见下表（单位：人）
（Ⅰ）求x，y；
（Ⅱ）若从高校A、C抽取的人中选2人作专题发言，求这二人是高校A、C各一人的概率．
| 高校 | 相关人数 | 抽取人数 |
| A | 18 | x |
| B | 36 | 2 |
| C | 54 | y |
（Ⅱ）若从高校A、C抽取的人中选2人作专题发言，求这二人是高校A、C各一人的概率．
考点：等可能事件的概率,分层抽样方法
专题：应用题,概率与统计
分析：（1）根据分层抽样的特点，可得
=
=
，解可得答案；
（2）根据题意，由组合数公式可得，从A、C抽取的4人中，选2人的可能情况数目，同理可得二人是高校A、C各一人的可能情况数目，由等可能事件的概率公式计算可得答案．
| x |
| 18 |
| 2 |
| 36 |
| y |
| 54 |
（2）根据题意，由组合数公式可得，从A、C抽取的4人中，选2人的可能情况数目，同理可得二人是高校A、C各一人的可能情况数目，由等可能事件的概率公式计算可得答案．
解答：
解：（1）由题意可得
=
=
解得x=1 y=3
（2）设高校A的小组成员为a高校C的小组成员为b，c，d
则从这4人当中抽取两人的，基本事件为（a，b）（a，c）（a，d）（b，c）（b，d）（c，d）共计6个基本事件
设二人分别来自AC高校的事件为A，则A事件包含的基本事件有（a，b）（a，c）（a，d）共计3个基本事件
则P（A）=
=
．
| x |
| 18 |
| 2 |
| 36 |
| y |
| 54 |
（2）设高校A的小组成员为a高校C的小组成员为b，c，d
则从这4人当中抽取两人的，基本事件为（a，b）（a，c）（a，d）（b，c）（b，d）（c，d）共计6个基本事件
设二人分别来自AC高校的事件为A，则A事件包含的基本事件有（a，b）（a，c）（a，d）共计3个基本事件
则P（A）=
| 3 |
| 6 |
| 1 |
| 2 |
点评：本题考查等可能事件的概率计算与分层抽样的方法，注意计算准确即可．
练习册系列答案
相关题目
在△ABC中，a、b、c分别是A、B、C的对边，面积S=a2-（b-c）2，则sinA=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
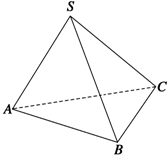如图所示，在三棱锥S-ABC中，SA⊥SB，SB⊥SC，SA⊥SC，且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3，三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3，类比三角形中的正弦定理，给出空间情形的一个猜想．